代达罗斯本可以从英国和瑞士的物理学家团队那里获取灵感。

他们从分形几何和国际象棋的策略游戏中汲取原理，创造出了他们所说的有史以来最难的迷宫。

在英国布里斯托尔大学物理学家菲利克斯·弗利克的带领下，这个研究小组在阿曼-比克尔平纹图案中产生了被称为汉密尔顿循环的路线，创造了复杂的分形迷宫。他们说，这些分形迷宫描述了一种被称为准晶体的特殊物质形态。

它的灵感来自于一个骑士在棋盘上的移动。

“当我们观察我们构建的线条的形状时，我们注意到它们形成了令人难以置信的复杂迷宫。随后迷宫的大小呈指数级增长，且数量无限，”弗莱克解释说。

“在骑士之旅中，棋子(向前跳两个格，向右跳一个格)在回到起始方格前只访问一次棋盘的每个方格。这是‘汉密尔顿循环’的一个例子，即通过地图的循环只访问所有站点各一次。”

准晶体是自然界中极其罕见的物质形态，是固体中有序和无序晶体的奇特混合。

在有序的晶体中 —— 如盐、钻石或石英 —— 原子以非常整齐的模式排列，并在三维空间中重复。你可以将这个晶格的一部分叠加到另一部分上，它们就会完美地匹配。

无序的或无定形的固体是指其中的原子都是乱糟糟的，包括玻璃和一些通常在地球上找不到的冰。

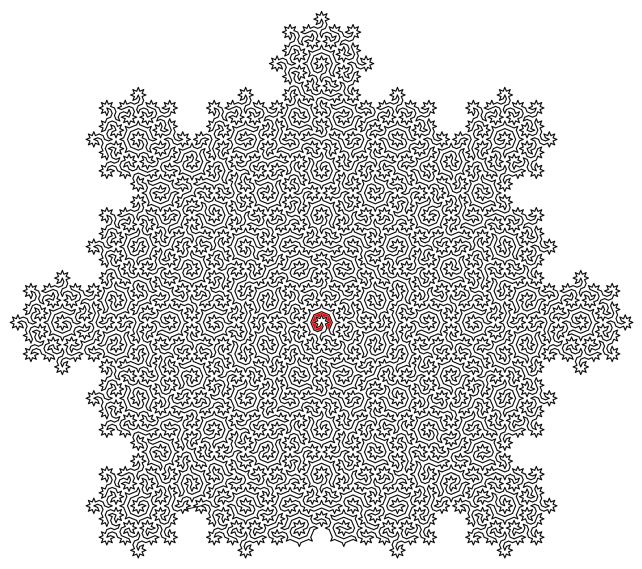
准晶体是一种原子形成图案但不能完美重复的材料。它可能看起来很自相似，但模式的重叠部分将不匹配。

这些相似但不相同的图案，与称为非周期平铺的数学概念非常类似，涉及不完全重复的形状图案。

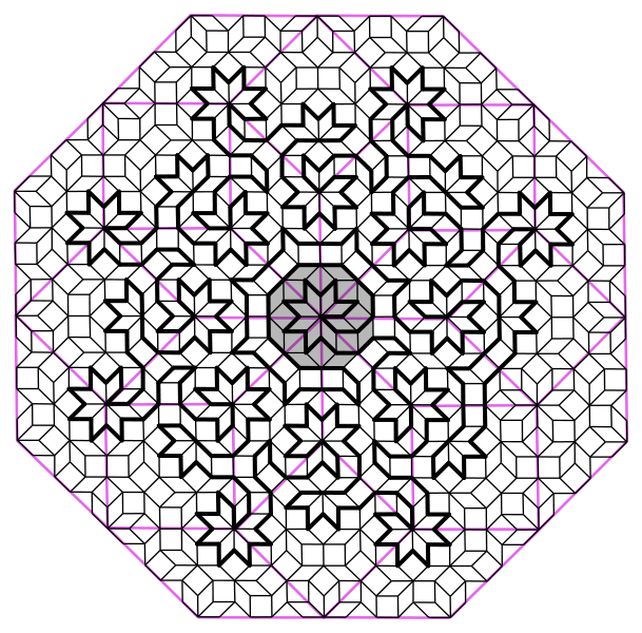
著名的彭罗斯拼图就是其中之一。Ammann-Beenker拼图是另一个例子。

弗莱克和他的同事，英国卡迪夫大学的物理学家Shobhna Singh和瑞士日内瓦大学的Jerome Lloyd，利用一组二维 Ammann-Beenker拼图，生成了他们认为描述准晶体原子模式的汉密尔顿循环。

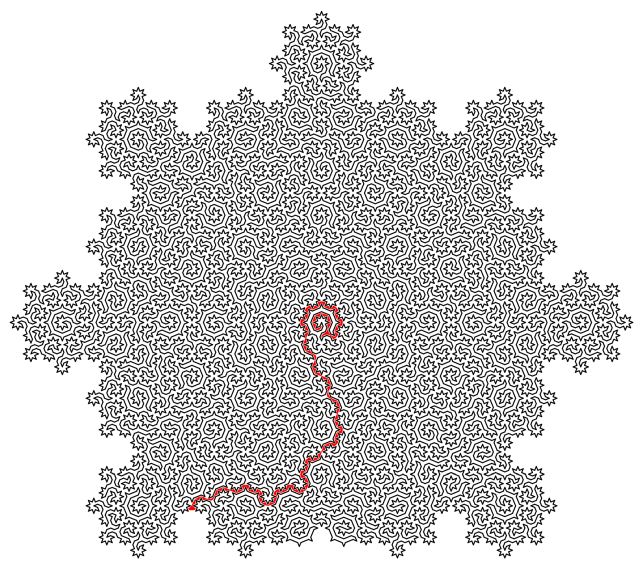
他们生成的周期只访问准晶体中的每个原子一次，将所有原子连接在一条直线上，这条直线永远不会交叉，而是从头到尾干净利落地持续下去。它可以无限缩放，产生一个称为分形的数学模式，其中最小的部分与最大的部分相似。

这条线自然产生了一个有起点和出口的迷宫。但这项研究的意义远不止让用餐时坐立不安的孩子开心。

首先，找到汉密尔顿循环是非常困难的。能够识别汉密尔顿解决方案的系统有可能解决许多其他棘手的数学问题，从复杂的寻路系统到蛋白质折叠。

有趣的是，这也暗示了通过吸附来捕获碳的可能性，这是一种工业过程，通过将液体中的分子粘在晶体上来吸收它们。如果我们能在这个过程中使用准晶体，那么柔性分子就可以沿着汉密尔顿循环更紧密地包裹自己。

Singh说：“我们的工作还表明，在某些吸附应用方面，准晶体可能优于晶体。”

“例如，弯曲分子将找到更多方式降落在准晶体的不规则排列的原子上。准晶体也很脆，这意味着它们很容易碎成微小的颗粒。这使它们的吸附表面积最大化。”

如果你碰巧有个牛头怪需要藏起来（迷宫），现在我们知道有人能帮忙了。

这项研究发表在《物理评论X》期刊上。