我的提问：例如单位分解（partition of unity）中的求和

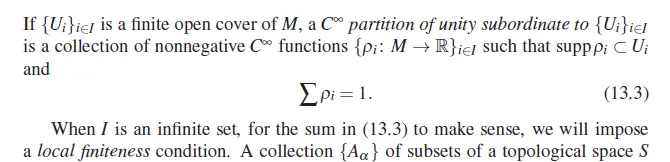
以及抽象代数中的多项式表达式。

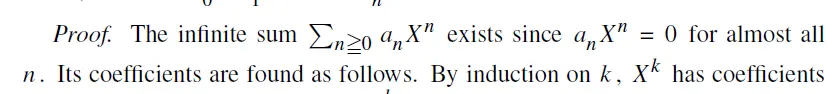
回答：拥有无限多项的求和（或者说更加正式的“级数”）需要一些额外的条件来保证他们“表现良好”（"well behaved"）。否则你可能得到像以下这样的悖论：

$$\begin{align} &S = 1 + 1 + 1 + \dots \\ &\Rightarrow 2S = 2 + 2 + 2 + \dots \\ &\Rightarrow 2S = (1+1) + (1+1) + (1+1) + \dots \\ &\Rightarrow 2S = 1 + 1 + 1 + \dots \\ &\Rightarrow 2S=S \\ &\Rightarrow S = 0 \end{align}$$

一般地，额外的条件包含，要求除了有限数量的项都为$0$（数学简称中的“几乎所有”）或者收敛条件来确保求和有一个极限值。

本问题问于2020年1月22号，当时我在读高三，提问的水平非常差😅，跟Peter Scholze这种高中就懂谱序列的没得比🙃。