作为一个不经常玩MC的MC老玩家，在一年前回归MC后，看到别人弄的各种花样的模组，我萌生了做个属于自己的模组的想法。作为一个MC魔改的新手，刚开始尝试制作模组并不容易，一是网上搜到的资料参差不齐，二是修改过程中需要改哪些参数，有的需要自己摸索，三是修改过程中会出现bug需要多次重启游戏进行测试。

本篇文章算是我人生中的第一篇游戏文章，我选择分享之前我特别感兴趣的《矿脉扩张》模组。所谓矿脉扩张，顾名思义就是将原本的矿脉扩大数倍不止，达到取之不尽用之不竭的程度。这又是众所周知的懒狗生存🤣，该模组可以说十分对胃那种喜欢挖矿的玩家，并且搭配上连锁挖矿每挖一次就爆出一大堆经验，可谓是十分解压😁。

我玩MC的时候就是挖矿总是挖得不够爽，煤矿还好一些，别的矿尤其是一些比较稀有的矿，如钻石矿一下就挖完了。我很想体验一下那种暴富的感觉，无论什么矿，都一挖一大把，钻石套、下界合金套全都轻松凑齐，然后拿钻石块、下界合金块搭房子😇。

于是有次在网上浏览模组时，我发现了有人分享了矿脉扩张模组，我第一次知道原来连矿脉分布都可以修改，当我怀着兴奋和期待试过好几个模组，最后结果都不如我所愿。网络上的矿脉扩张模组首先很少，并且矿脉扩张的幅度很小，完全没达到我想象的效果。同时，有的模组只是扩张了某个单一矿脉，如下界合金，其它都没变。本着既然别人没有做我想要的，那就自己做个自己喜欢的想法，我下手DIY了一个自己的矿脉扩张模组。

模组效果图如下：

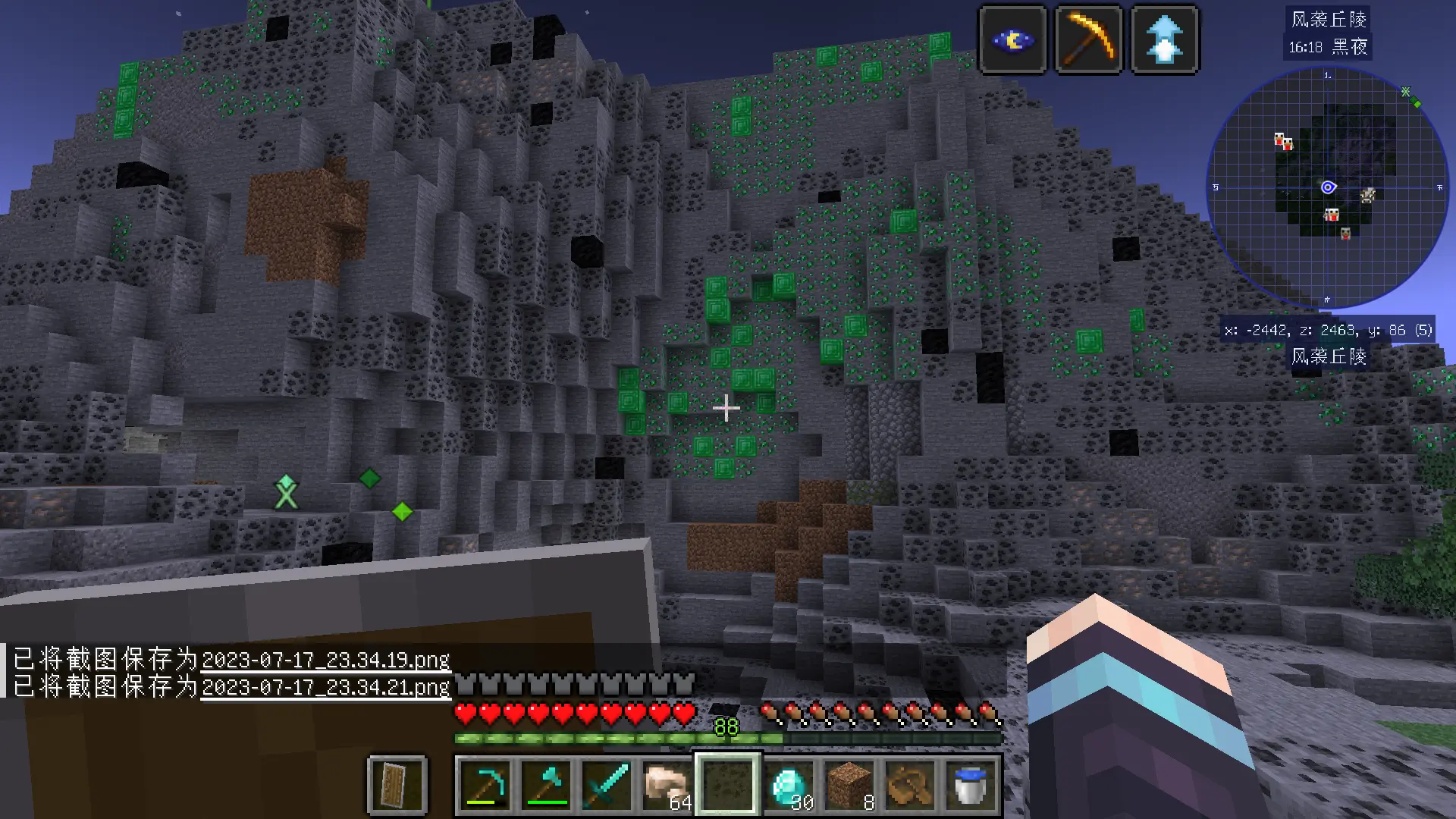
首先更多的煤矿石，以及数不清的绿宝石矿，再也不用担心跟村民们交易不够绿宝石啦😁！接着，你可以看到矿脉中夹杂着煤块和绿宝石块。那是因为矿脉密度太高了，以致于都凝结成固体了😎。接着铁矿也是在地面上即随处可见，再也不用”下矿“就能得到铁了，或者说以后在地表也能下矿啦😏！

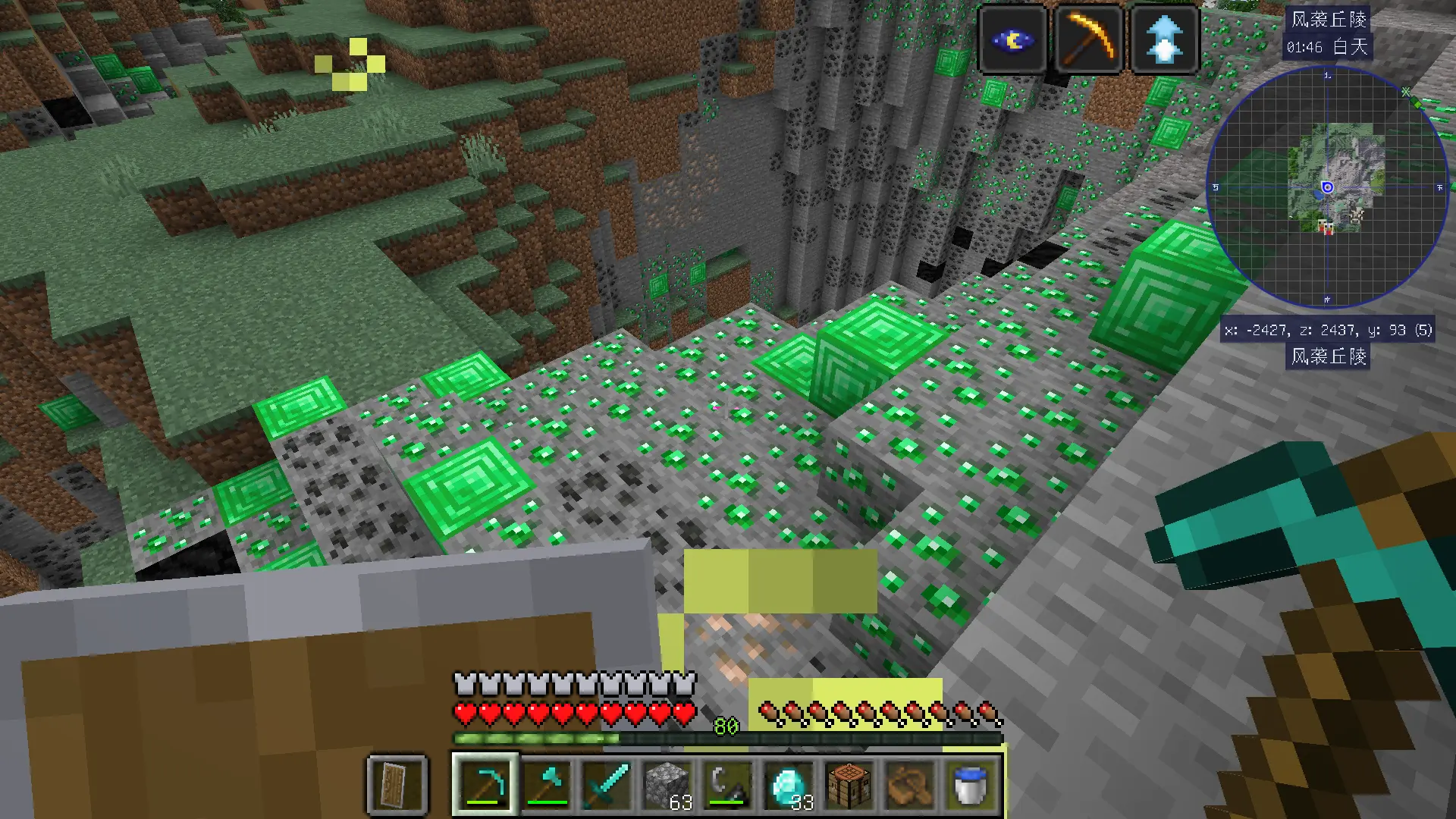
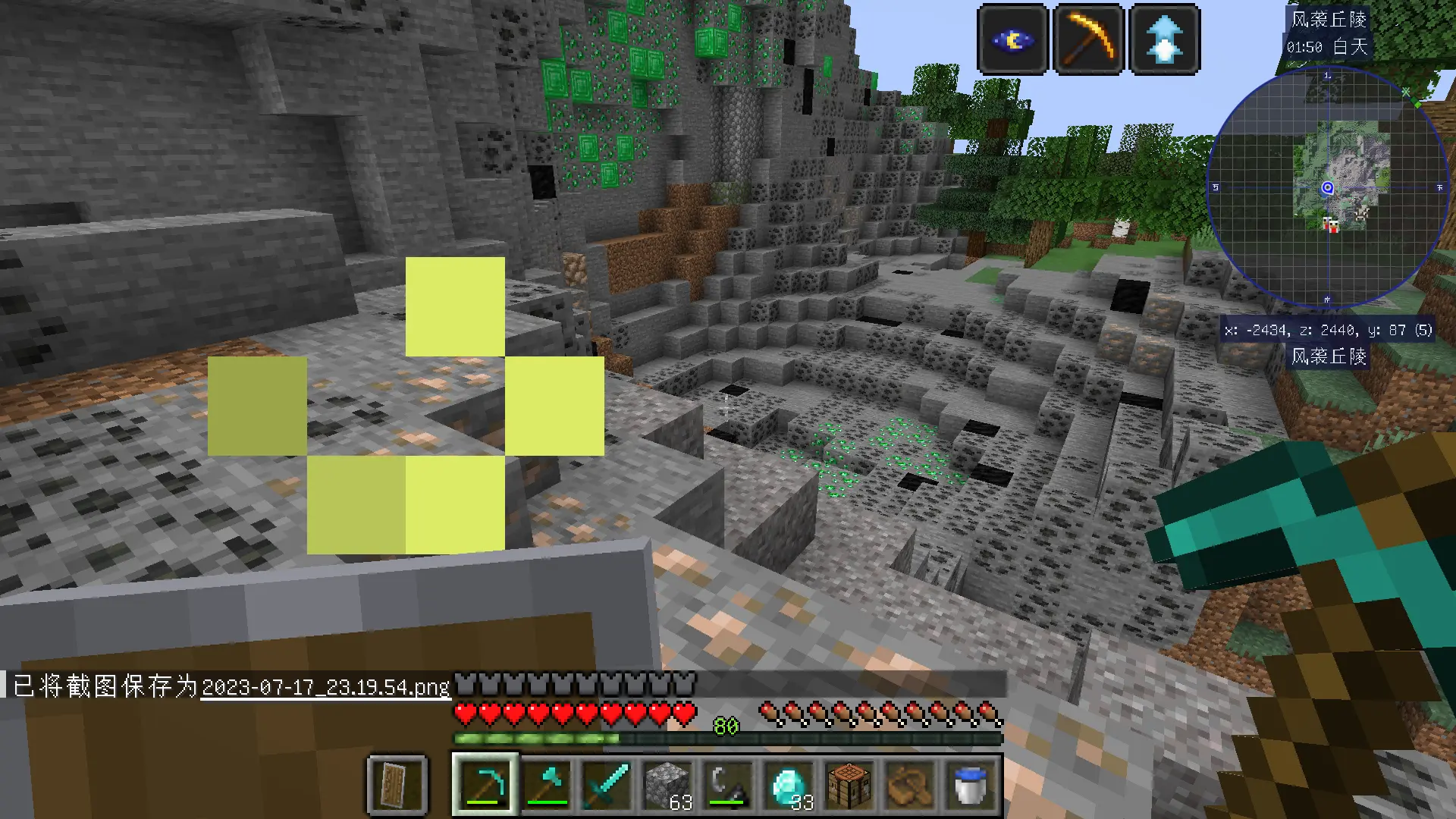
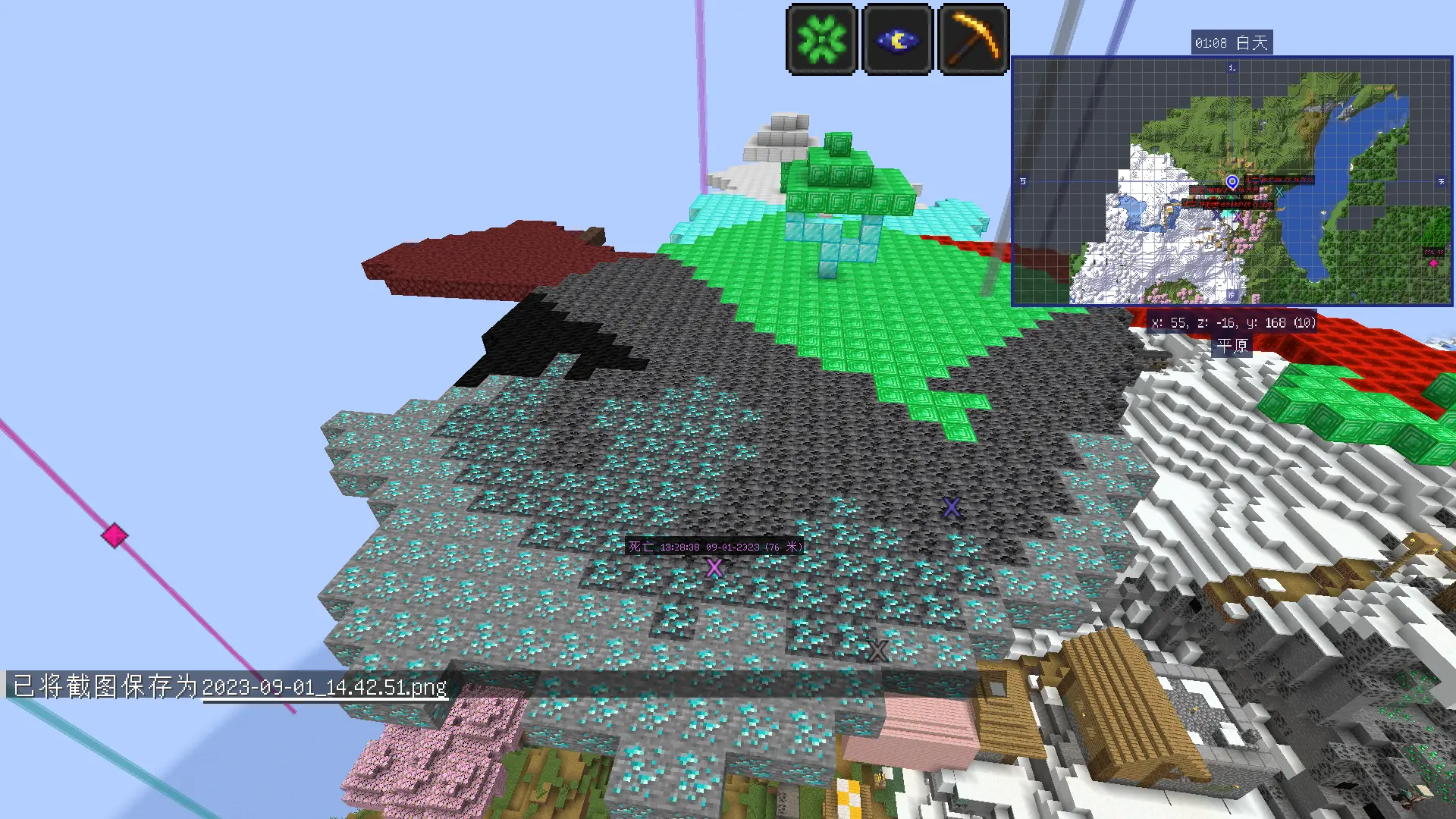
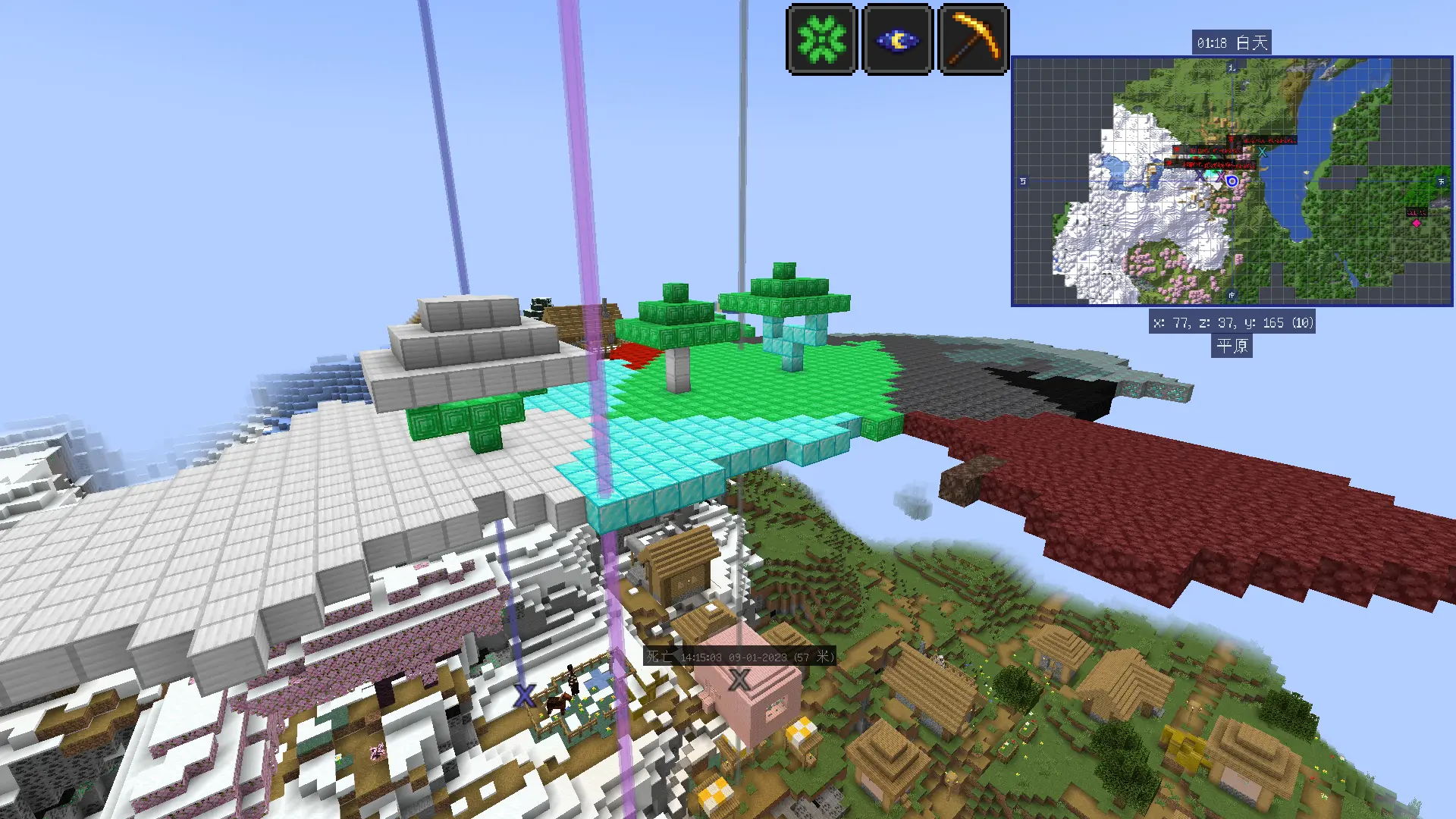
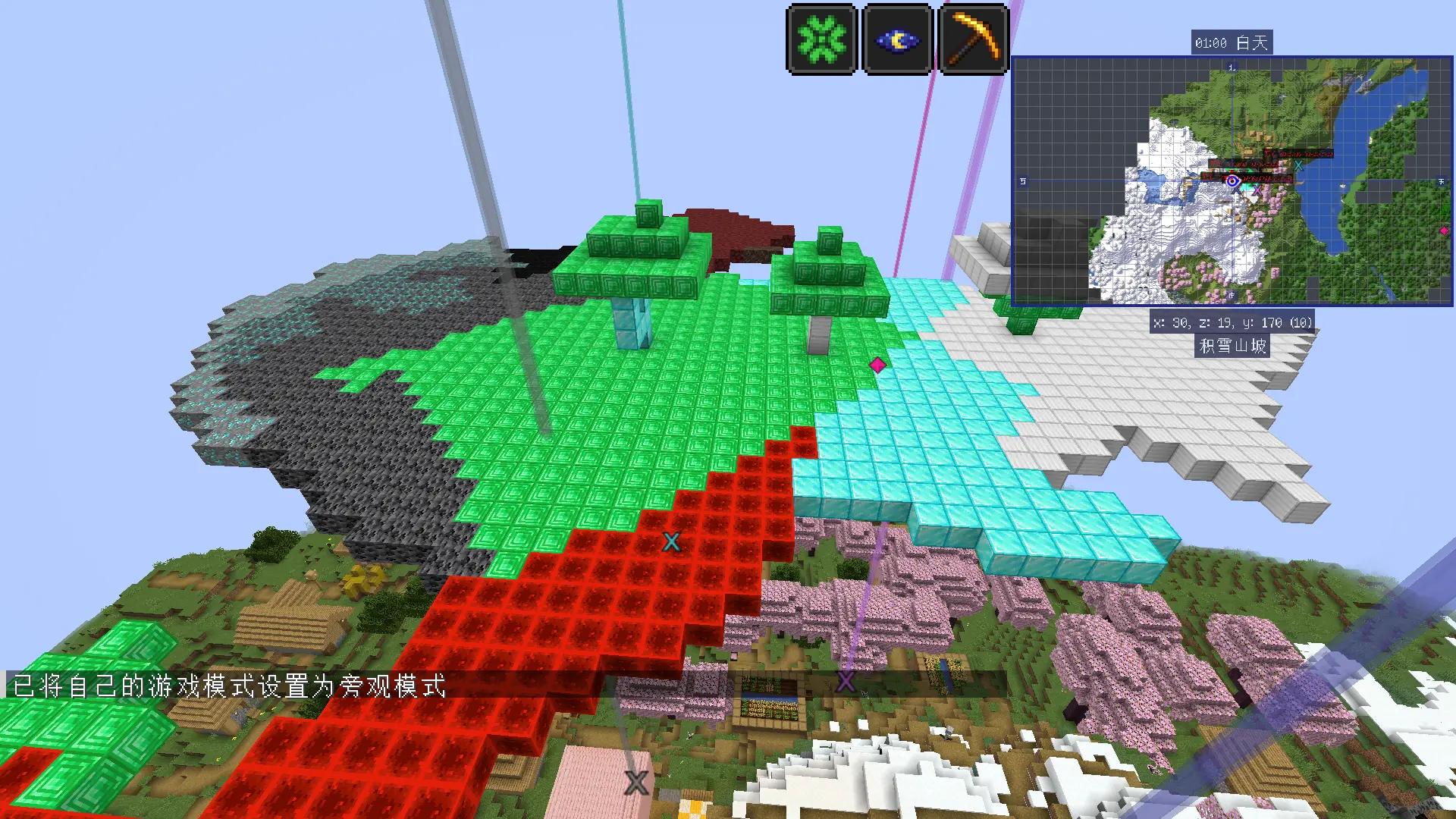
在地表上矿都已经多到溢出来了，那地底下岂不是更离谱😎？？！多图预警......

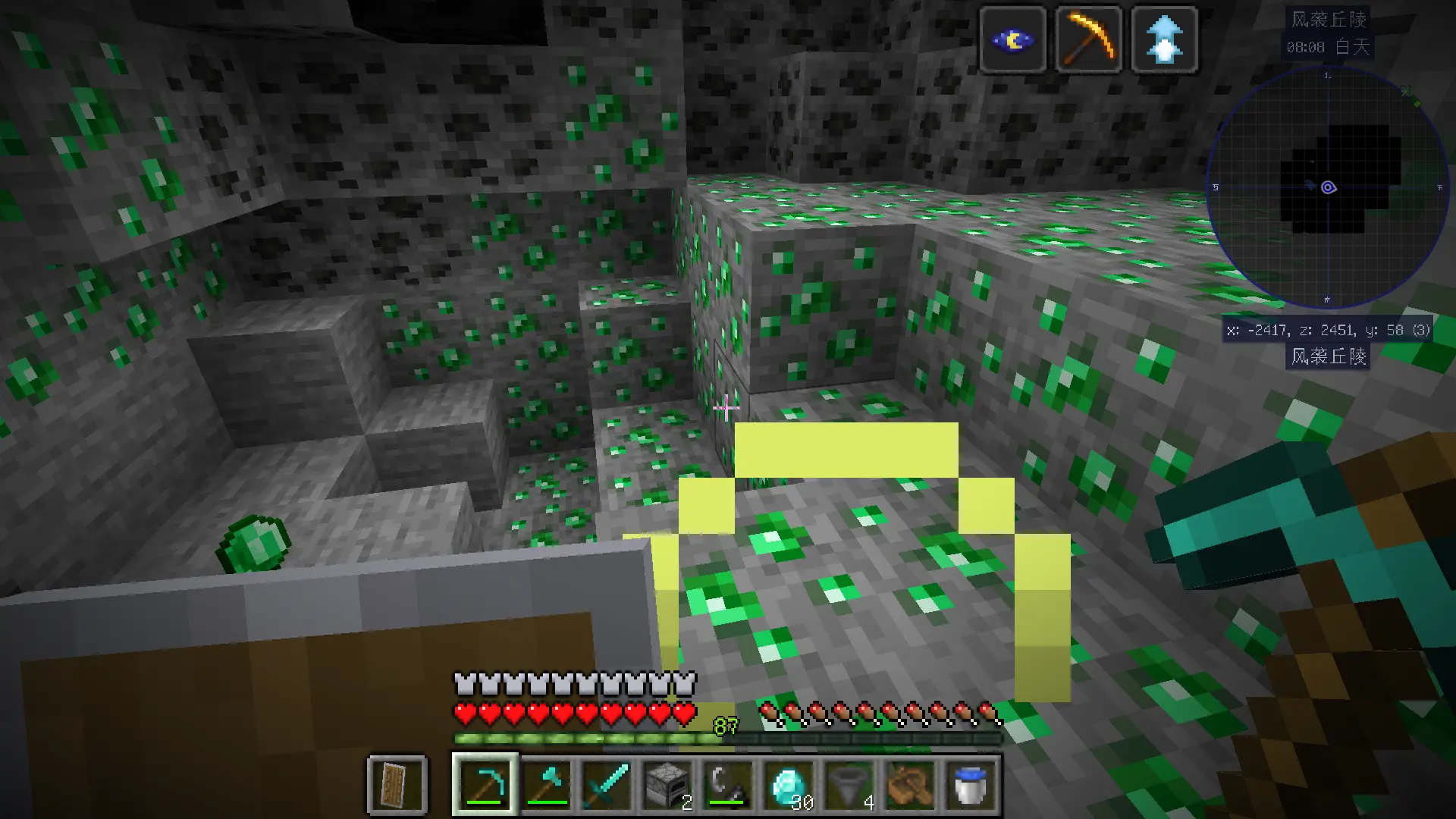
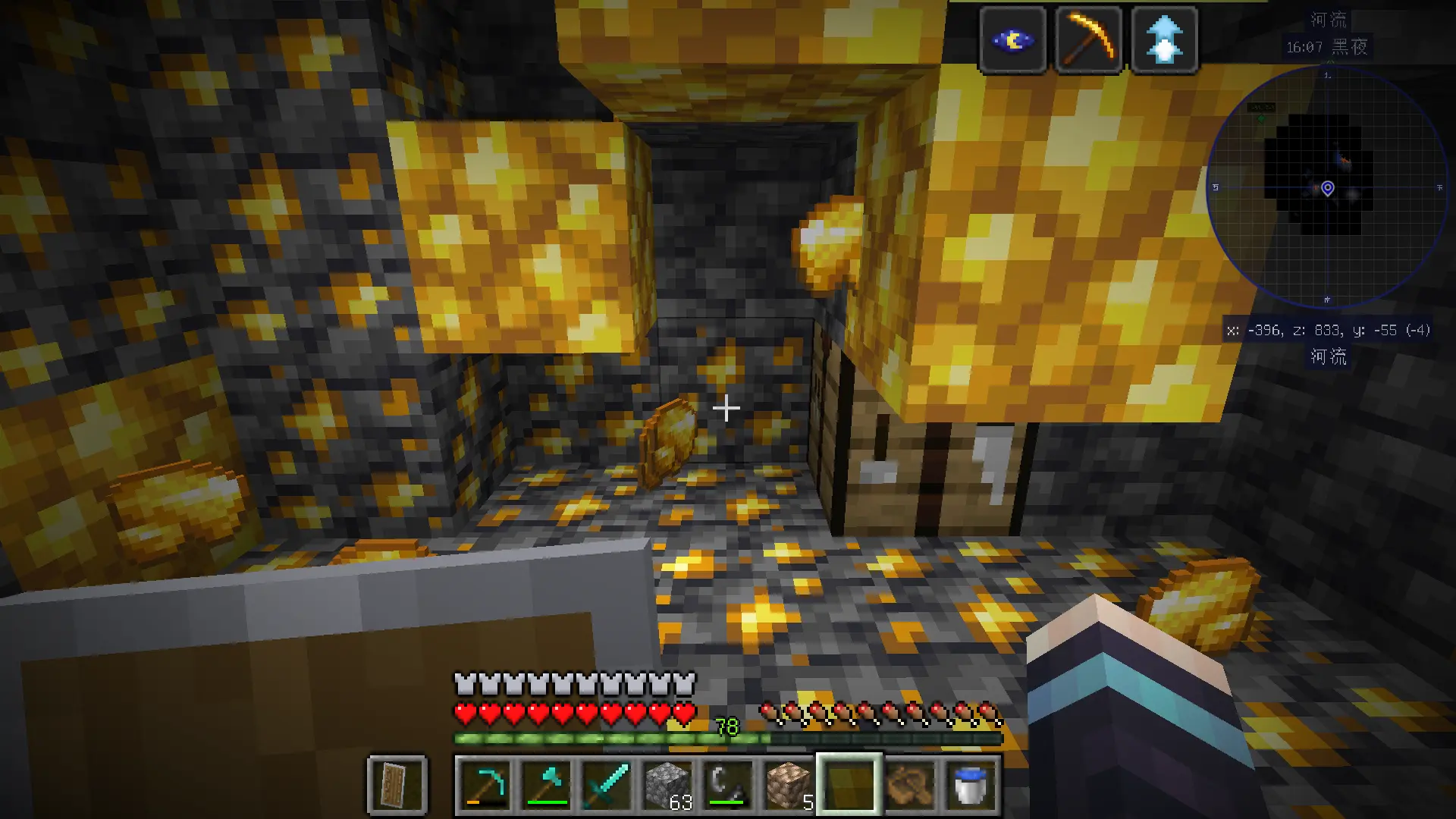
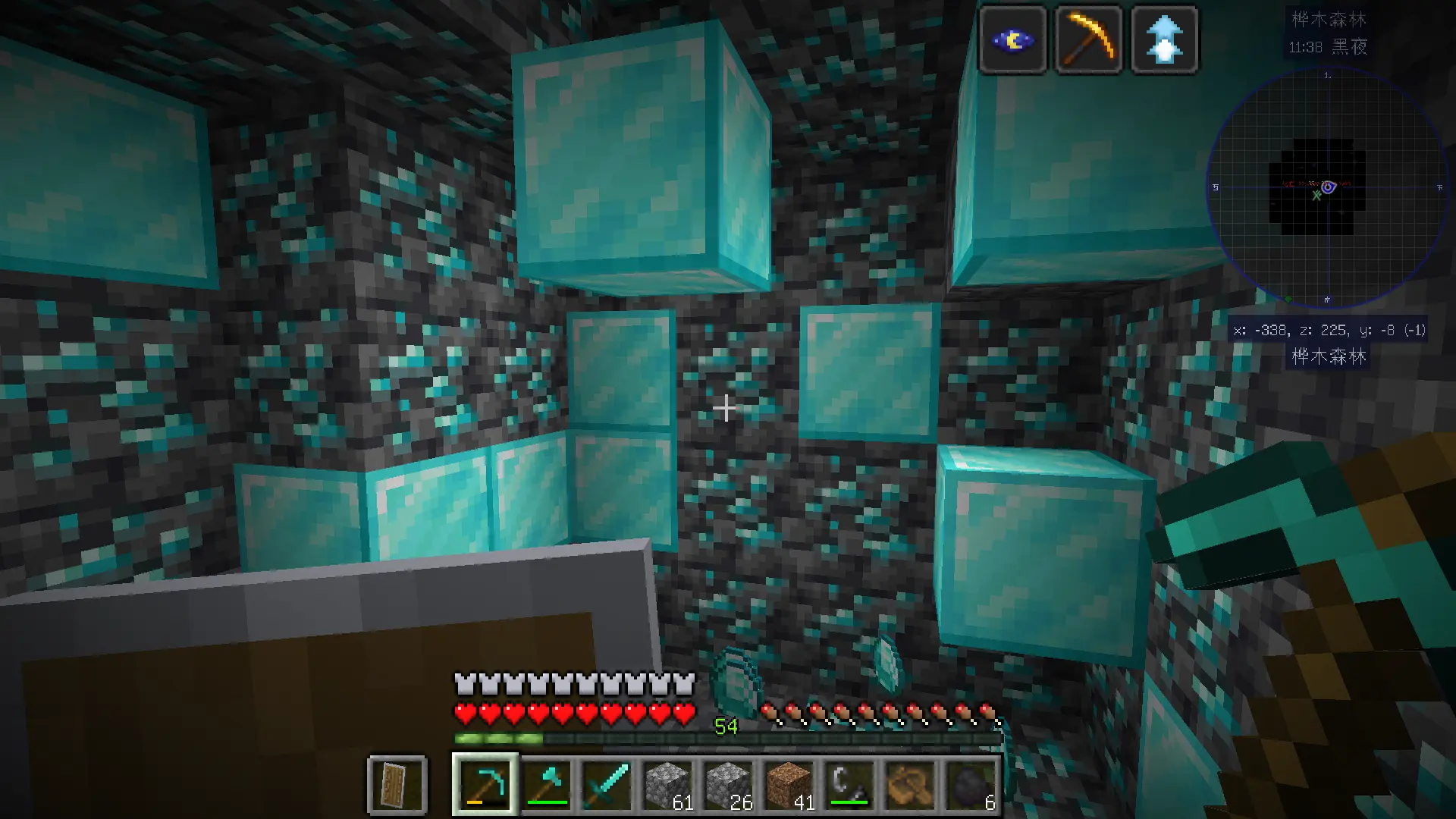
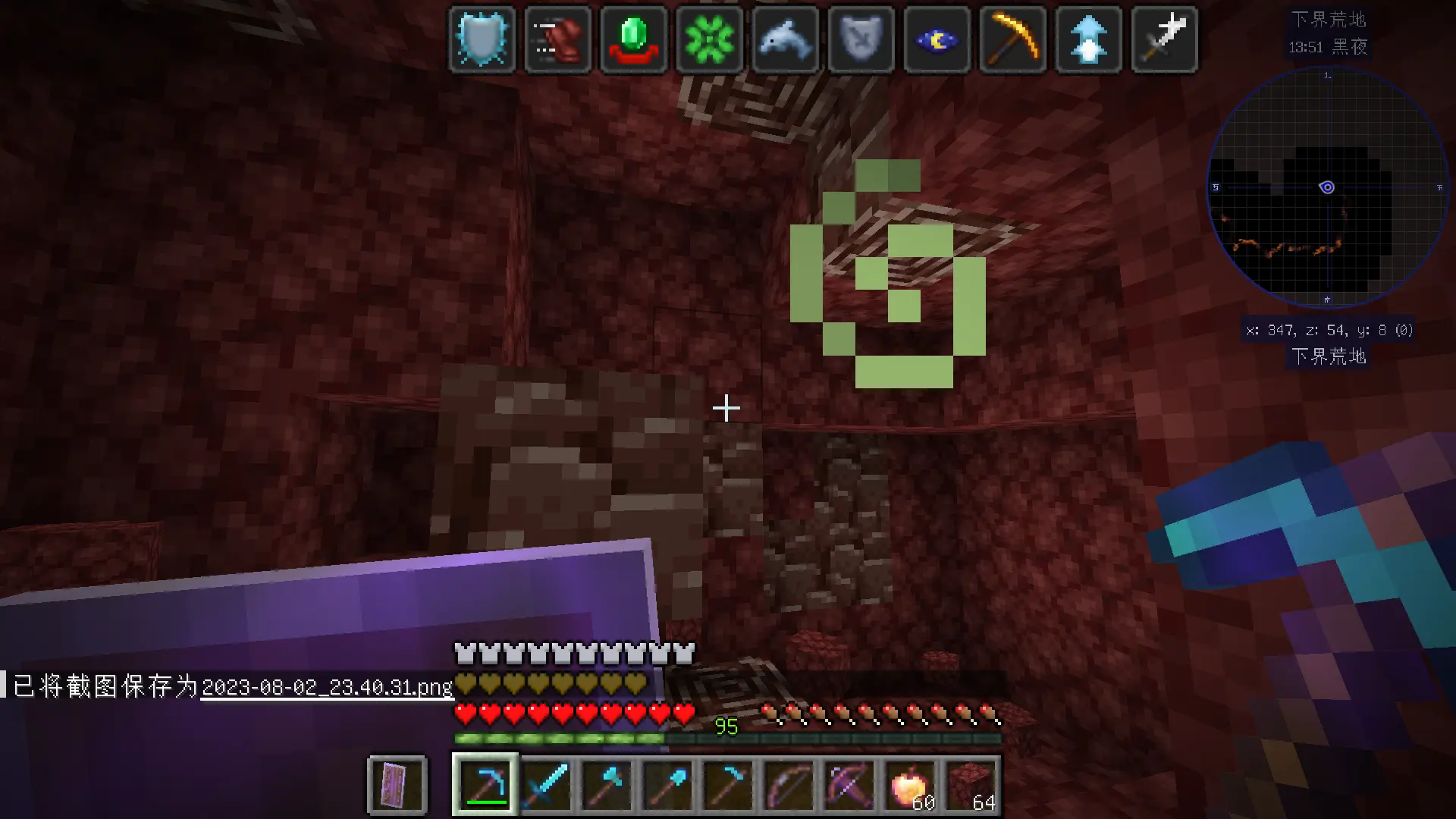
可见地底下，黄金遍地，钻石块满地像垃圾一样乱堆，远古残骸一大坨连在一起😇。加上连锁挖矿，一挖一大把，猛猛解压。不开连锁挖矿，给你锻炼手力和耐力，看你能挖多久挖多少😄。

勤劳矿工一天下来，收获满满🤗！

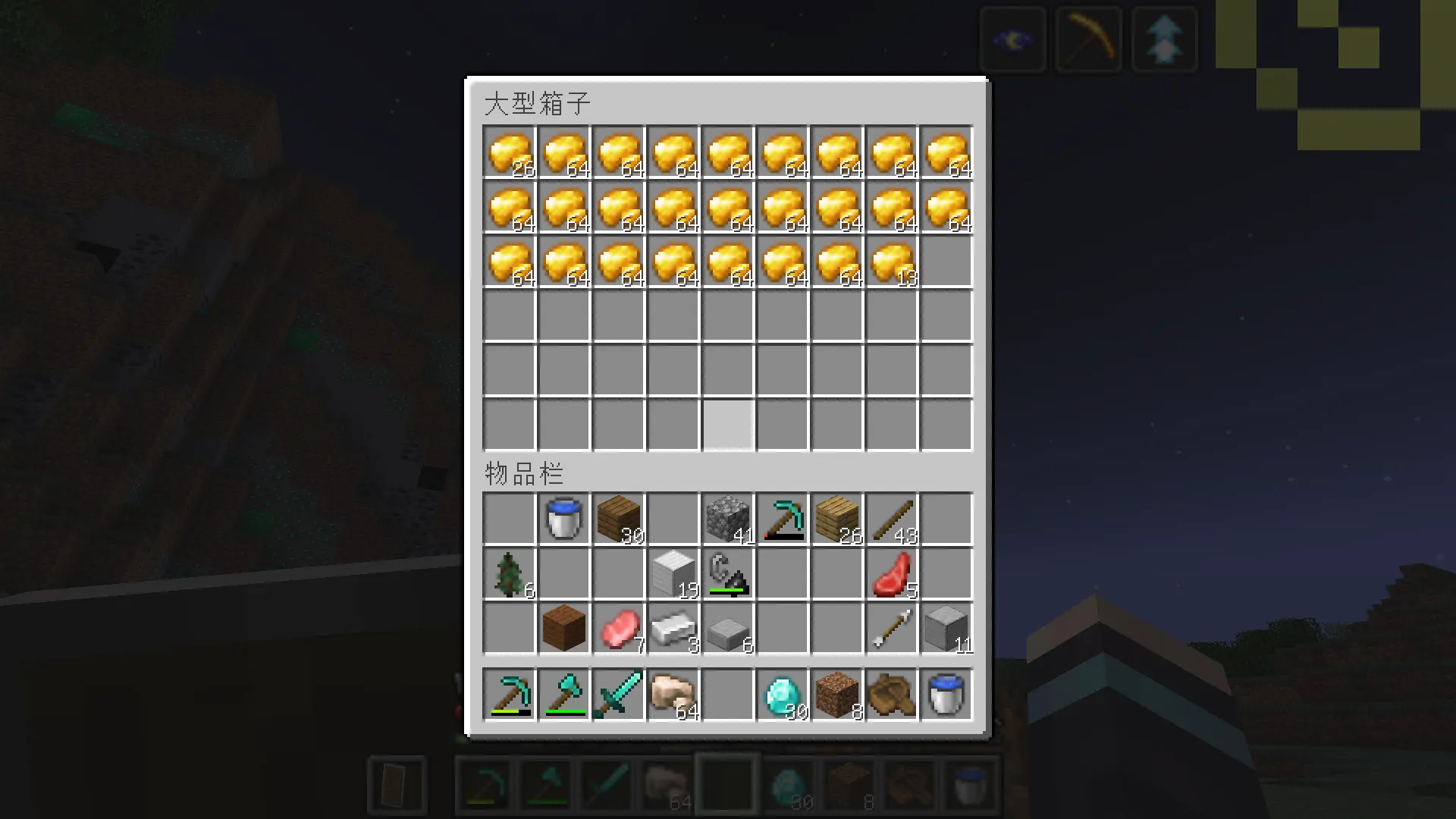
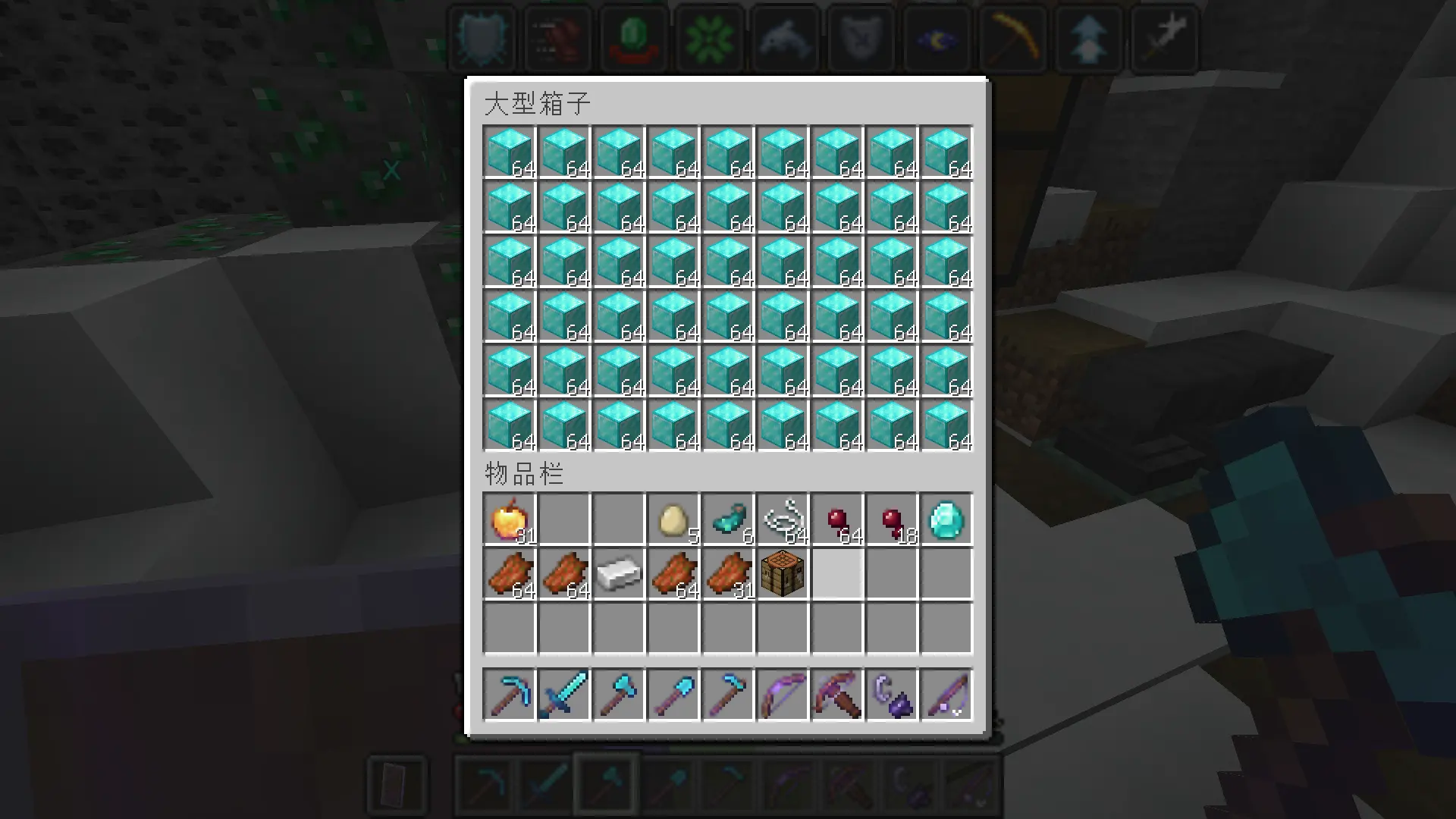
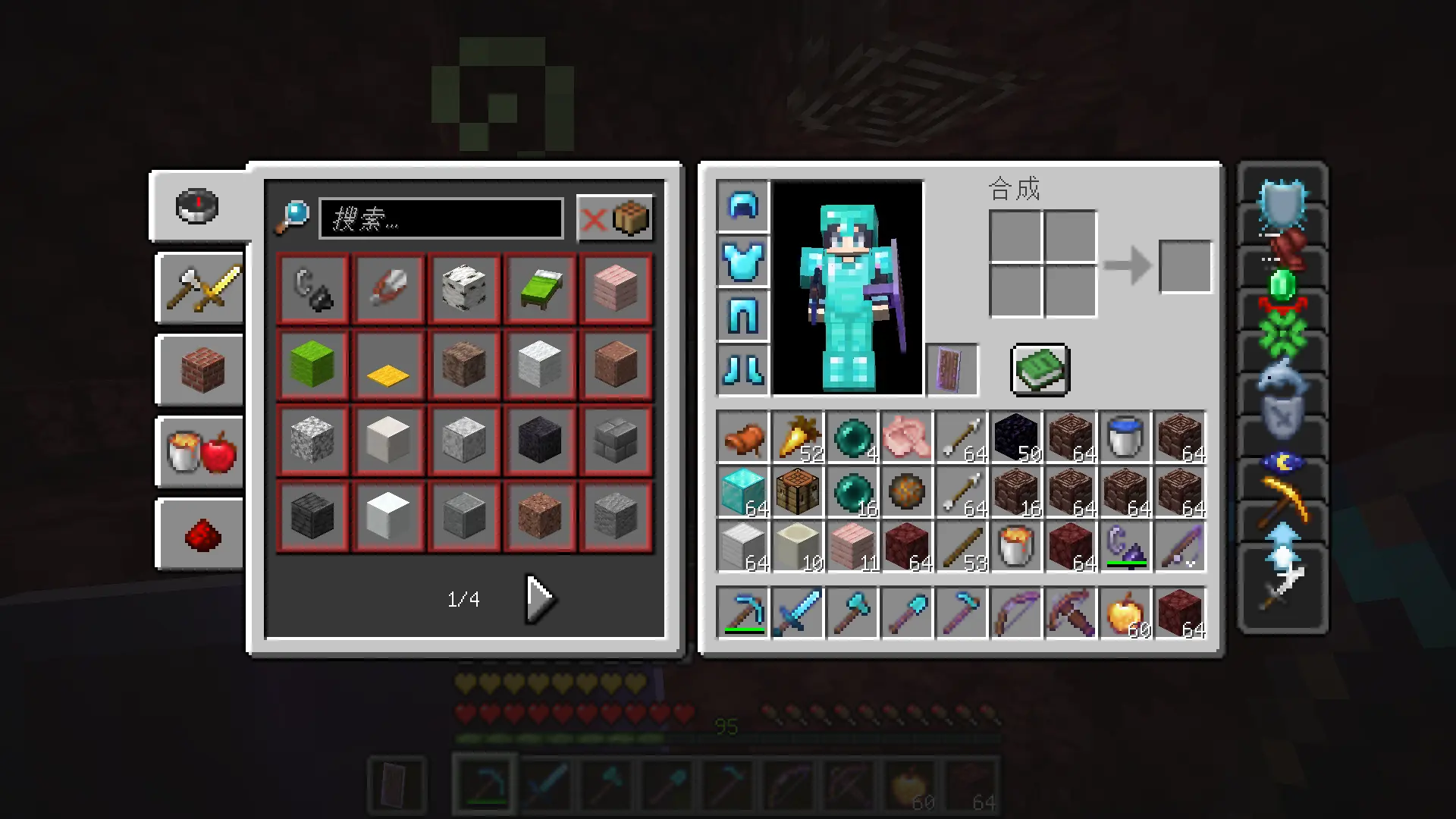
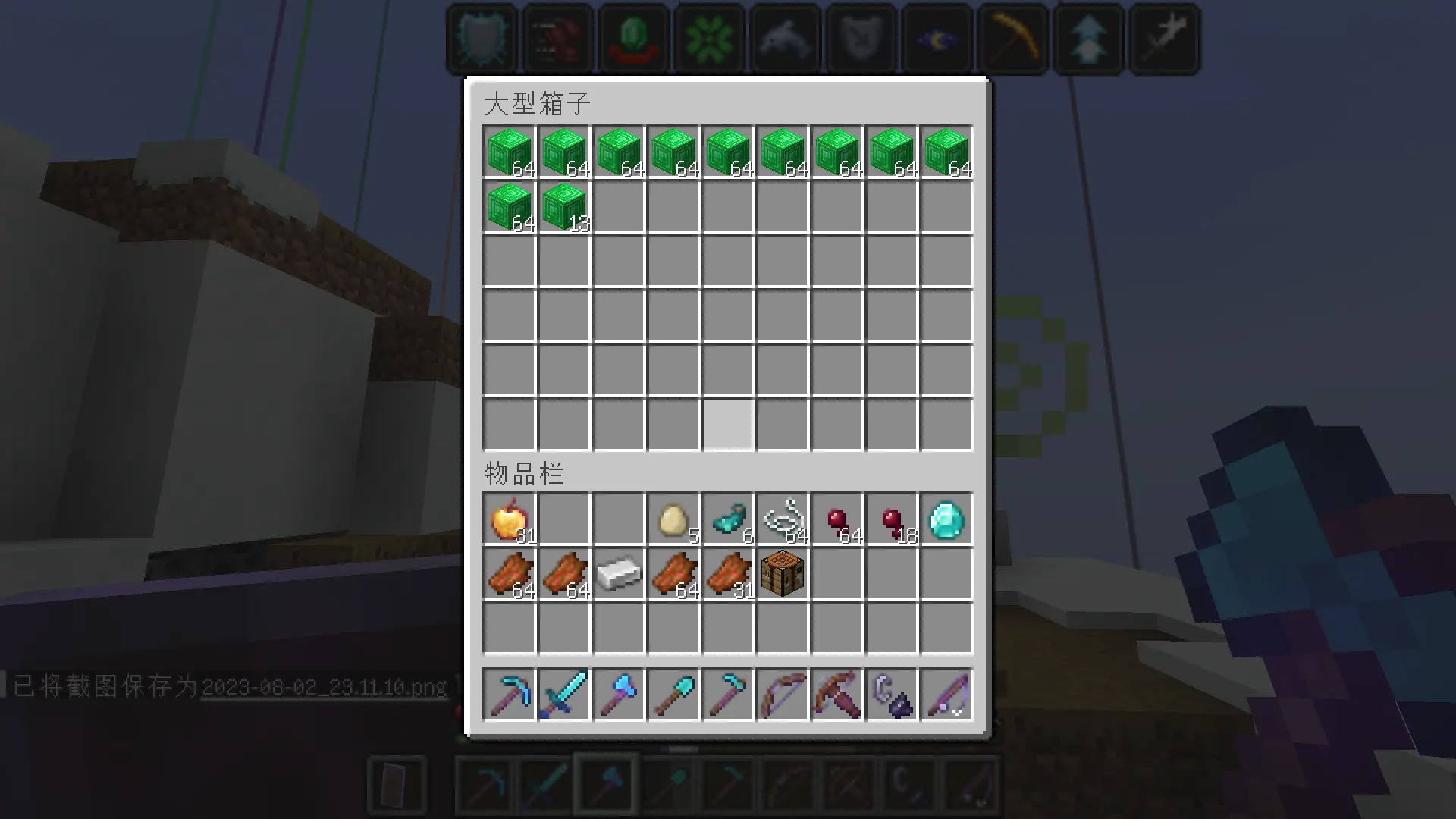
这么多东西，得用多少个熔炉才够烧啊？？😱

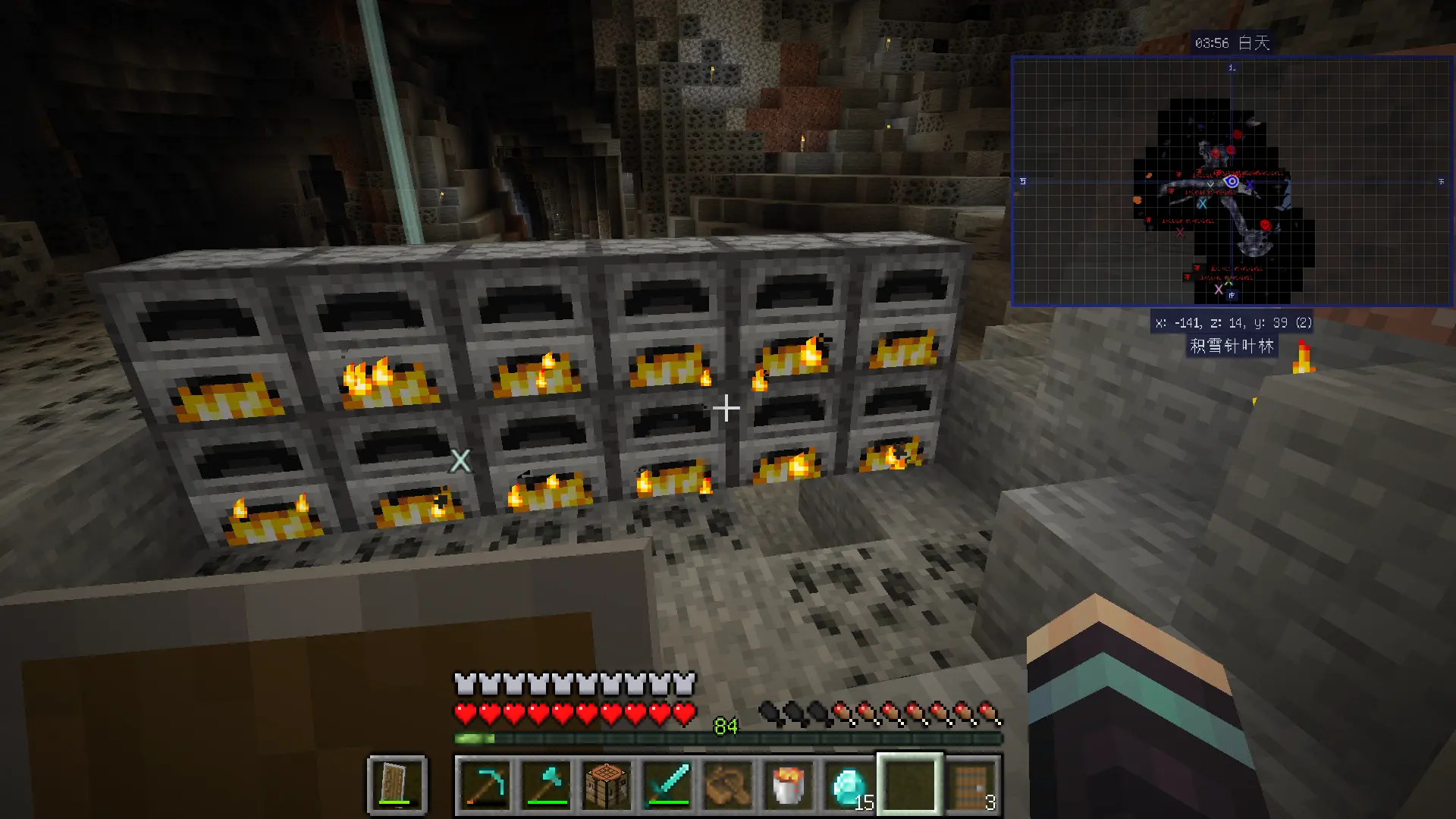
终于实现了拿钻石块、绿宝石块、矿石建东西的梦想啦😃！

本篇完，在下篇中我将会分享矿脉扩张模组的技术细节。关于模组下载，请看MC自制模组之矿脉扩张模组下载，感兴趣的小伙伴可以下来玩玩😃。