评审8年终获发表,数学天才望月新一证明abc猜想,全球只有十几个数学家读懂但争议未消
abc猜想,数学界悬而未决的重要猜想,它的证明过程经过8年的同行评审,终于要在期刊上发表了。
论文作者是日本的天才数学家望月新一,他33岁起就在京都大学担任数学教授。

这一次望月新一的证明,全篇超过600页,2012年就已发表,但足足经过了8年的同行评审才通过,期间开过多次研讨会——但依然有很多数学家无法理解。
据说,这篇论文全球只有十几位数学家深入研究了证明过程。
许多数学家根本无法指出证明过程是对是错,因为根本看不懂。

4月3日,日本京都大学召开了新闻发布会,宣布望月新一证明了它。包括Nature等在内的权威科学传媒组织,也这一重要进展进行了报道。

望月新一没有出席昨天的发布会,他的另外两位同事说,当他知道自己的论文被接收,终于松了一口气。多年来他从未在公众场合露面。
但也不是没有争议,因为当初接收论文的期刊——日本的PRIMS,主编正是望月新一本人。
如果他的证明是正确的,那么将彻底改变数论。
同时也正因为如此,才有了学界长达8年的争论。
什么是abc猜想?
abc猜想,最初由法国数学家约瑟夫·奥斯特莱和大卫·马瑟,在1985年提出。
并且一经提出,abc猜想就成为数论领域的重要猜想之一。
只是和哥德巴赫猜想不同的是,向大众说明abc猜想本身,就是一个复杂的过程。
大概如下:
有三个互质正整数a、b、c,且c=a+b。所谓互质,即它们的最大公约数是1。
因此8 + 9 = 17、5 + 16 = 21是符合条件的一组数字,但是6 + 9 = 15不是。
接着,我们把abc的质因数都提取出来,比如5、16、21的质因数是5、2、3、7,这些质因数相乘的结果为210,这个数比原来的三个数大得多。
又比如5、27、32,它们的质因数是5、3、2,相乘结果为30,就比32小。
但第二种情形极为罕见。如果a和b都是小于100的数,我们能找到3044个符合条件的abc组合,其中只有7组满足第二种情形。
而abc猜想要证明的,就是符合第二种情形的abc组合,只有有限个。
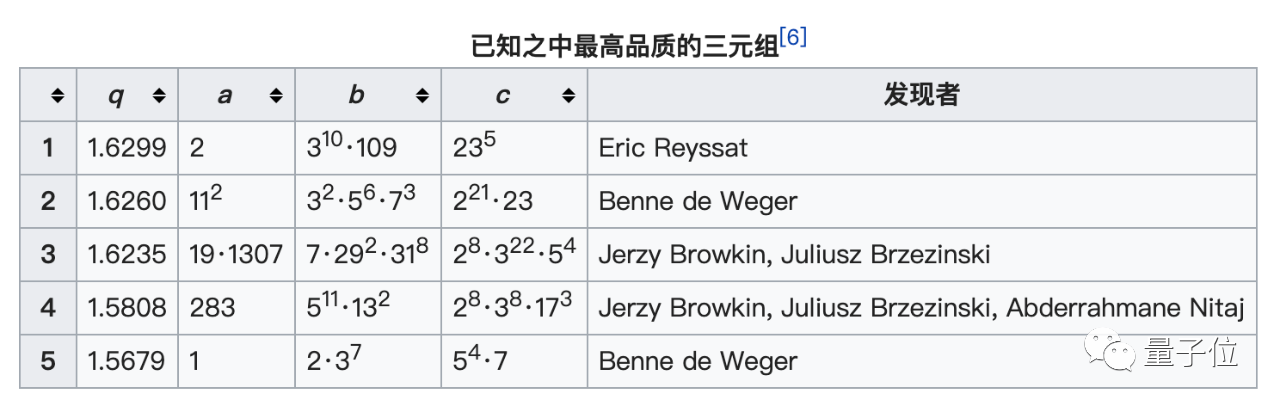
数学家们把abc的质因数乘积记作rad(abc)。用严谨的数学语言来表述就是:
对于任何ε>0,只存在有限个互质正整数的三元组(a, b, c),c = a + b,使得:c > rad(abc)1+ε
费马大定理迎刃而解
在人类短期内没法证明的abc猜想的情况下,科学家们想到了一个办法,就是用计算机暴力解决,从小到大依次寻找符合abc猜想第二种情形的组合。
由此衍生出了一个分布式计算项目ABC@Home,就是通过全球各地的电脑穷举计算符合abc猜想条件的三元数组。到2014年5月,人们已经验证了2380万个组合。
虽然有无限个例子或反例不能解决abc猜想,但是数学家希望借着该计划发现的三元数组的分布模式。
之所以花费大量计算资源去验证,是因为abc猜想在数学界有着重要意义。
和黎曼猜想一样,很多数学领域后续的一些假设都依赖于前者。如果前者得到证明,后者就能轻易得出。
abc猜想的形式是a+b=c,著名的费马大定理形式是xn+yn=zn,二者非常相似,实际上二者也是强关联。
如果abc猜想为真,那么费马大定理也可以轻松证明。
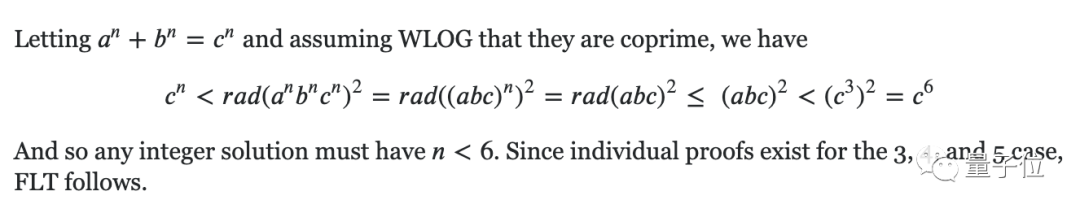
当年费马一句“空白太小写不下证明”,让这一问题从1637年一直拖到1995年才得以解决。
而通过abc猜想来证明费马大定理的方法,真的能让空白处就能写下证明过程。
所以望月新一这一次,真的做到了吗?
证明过程极具争议
望月新一发表了4篇论文来证明这一猜想,他把自己的研究成果叫做“宇宙际Teichmuller理论”。
按照望月新一的说法,该理论是用于椭圆曲线数字场的Teichmuller理论的算术版本,里面包含了像霍奇剧院(Hodge theaters)这样奇怪的名字。

望月新一的理论并未得到学界广泛认同,600多页的证明被来自德国波恩大学的两位德高望重的数学家质疑。
2018年菲尔兹奖得主、马普所数学研究所所长Peter Scholze说:“我认为abc猜想仍未解决,任何人都有机会证明这一点。”

Scholze和他的同事Jakob Stix还曾发表一篇报告,指出在望月新一第三篇论文中“推论3.12”证明过程从根本上来说是有缺陷的。
而该推论对abc猜想的证明至关重要。
和其他部分引理的证明不同,3.12的证明尤其长,总共有9页。Scholze认为这9页证明达到了根本无法遵循逻辑的地步。
Scholze在2018年到京都大学进行了为期一周的访问,与望月新一探讨了这个问题,但双方谁也说服不了谁。
Scholze说:“我认为,除非望月新一进行一些非常实质性的修改,并更好地解释这一关键步骤,否则不应该将其视为证明。”
“我真的没有看到一个使我们更接近abc猜想证明的关键思想”,Scholze还补充道。
望月新一的论文也引起了陶哲轩的关注,在当年论文发表的第一时间,陶哲轩就在个人博客中谈到的自己看法,并给出了另一种启发式证明方法。
望月新一研究领域并不是陶哲轩的擅长,所以他之后一直回避对此评论。
这篇论文被期刊接收,并不是abc猜想的终点,也无法让数学家站到望月新一这一边,新的争论还会继续下去。
关于望月新一
最后,简单介绍一下这位日本天才数学家。
望月新一,1969年出生于日本东京都,5岁随父母前往纽约,16岁就进入普林斯顿大学,3年读完本科,23岁获得博士学位,33岁成为京都大学教授。

他现在是京都大学数理解析研究所教授。研究数论,包括算术几何,霍奇理论和远阿贝尔几何。
有意思的是,还有人曾猜测,望月新一就是比特币发明人“中本聪”。
不过这种猜测的疑点很多,因为比特币用到的密码学不是望月新一的研究方向,而且他作为一个纯粹的数学家,对现实世界的问题也不太关心。
最后的最后,如果你对望月新一这一abc猜想证明有其他看法,也欢迎告诉我们。
参考资料:
本文转自微信公众号量子位
暂无评论,来发布第一条评论吧!