我的提问：令$X,Y$是概形。令$X\rightarrow Y,X\rightarrow X, Y\rightarrow Y$为概形态射。为什么态射$U\times_{X}X\rightarrow U\times_{Y}Y$是$X\rightarrow X\times_{Y}Y$通过$U\times_{Y}Y\rightarrow Y$的基变换。

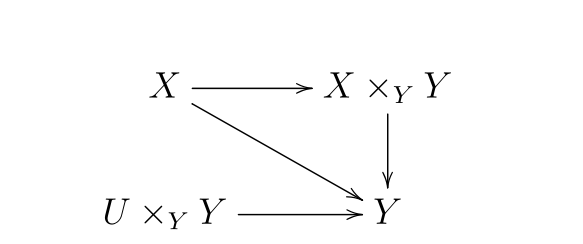
这是我尝试的图，其中三角形是交换的。但是我发现$(U\times_{Y}Y)\times_{Y}(X\times_{Y}Y)=U\times_{Y}X\times_{Y}Y=U\times_{Y}X$，即我无法得到想要的$U\times_{X}X$。我这是犯了什么错误？

这是问题的上下文，来自朱歆文的论文Affine Grassmannians and the geometric Satake in mixed characteristic (arXiv link)：

引理 A.2. 对任何代数空间的平展态射$X\to Y$，由$\sigma_X$导出的相对Frobenius态射$X\to X\times_{Y,\sigma_Y}Y$是一个同构。

证明：我们首先假设$X$是一个概形。那么$X\to X\times_{Y,\sigma_Y}Y$是一个概形的、根本的、平展的、满的（schematic radical étale surjective）映射，并且因此由[EGAIV，定理 17.9.1]是一个同构。

对于一般的$X$，选择一个通过概形$U$的平展覆盖$U\to X$。然后我们有$U\to U\times_{X,\sigma_X}X\to U\times_{Y,\sigma_Y}Y$，其中第一个映射和复合的映射都是同构。因此，第二个映射也是同构。注意到$U\times_{X,\sigma_X}X\to U\times_{Y,\sigma_Y}Y$其实就是$X\to X\times_{Y,\sigma_Y}Y$沿着平展覆盖$U\times_{Y,\sigma_Y}Y\to Y$的基变换。因此，$X\to X\times_{Y,\sigma_Y}Y$也是一个同构。

回答：图比你正在使用的要复杂些。首先，我们有一个定义$X\times_{Y,\sigma_Y} Y$的基变换图如下：

$$\require{amscd}\begin{CD} X\times_{Y,\sigma_Y} Y @>>> Y\\ @VVV @VV{\sigma_Y}V \\ X @>>> Y \end{CD}$$

态射$X\to X\times_{Y,\sigma_Y} Y$是由单位态射$X\to X$，态射$X\to Y$，以及纤维积的泛性质所导出的。

定义$U\times_{Y,\sigma_Y} Y$的图如下：

$$\begin{CD} U\times_{Y,\sigma_Y}Y @>>> X\times_{Y,\sigma_Y} Y @>>> Y\\ @VVV @VVV @VV{\sigma_Y}V \\ U @>>> X @>>> Y \end{CD}$$

现在通过映射$U\times_{Y,\sigma_Y} Y\to Y$基变换整个第一个图加上导出的态射$X\to X\times_{Y,\sigma_Y} Y$来得到断言的映射。

本文是What is base change map ?的灵感来源，正是因为有了这个提问，才有那篇短文的进一步解释。