抽象代数中如何执行归纳法?
我的提问:
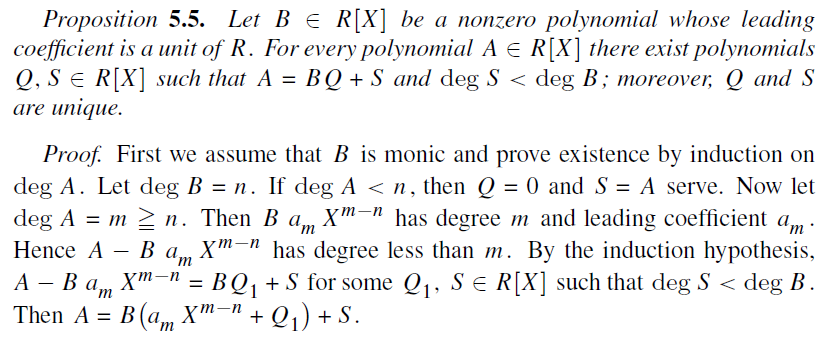
我无法理解在这个证明中,归纳法这个步骤是如何进行的。有人能帮帮我吗?感谢!
回答:令$n = deg B$。他们通过对$m = deg A$做归纳法来证明那个陈述。基本情况是$m < n$。如果$m \geq n$,然后他们找到另一个多项式$A'$,在这种情况下,$A' = A - B a_m X^{m - n}$,并且它有比$m$更小的阶数。所以我们可以通过归纳假设来处理它。$A′$的商和余数表达式是用于找到$A$的。
我想有两件事你可能会觉得困扰,以及为什么你没有认出归纳法。首先,基本情况不仅仅是一种情况,而是一堆情况。这里请注意,这是基本的:证明中的归纳步骤仅适用于$m\geq n$。同时注意,在这种情况下,证明$m=1$的工作量并不比证明$m<n$小:对于所有这些情况,这都是一行证明。
你可能会觉得困扰的第二件事是,我们不仅对$m-1$使用归纳假设,对任何阶数严格小于$m$的多项式也使用归纳假设。这被称为完全归纳法或强归纳法:在归纳步骤中,你假设的是,命题不多于$m-1$时都是真的,而不仅仅是$m-1$。这在维基百科的“归纳法”页面上得到了很好的解释。
暂无评论,来发布第一条评论吧!