My question: For example, the sum in the partition of unity,

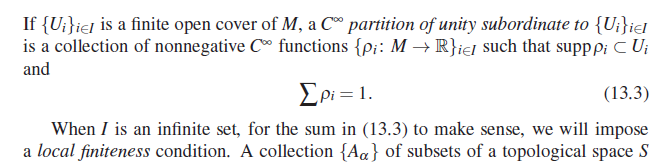
and the polynomial expression in abstract algebra.

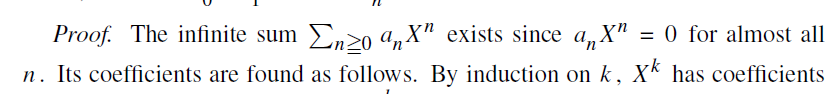
Answer: Sums with an infinite number of terms (or "series" in more formal terms) need some extra conditions to make sure they are "well behaved". Otherwise you can get paradoxes like the following:

$$\begin{align} &S = 1 + 1 + 1 + \dots \\ &\Rightarrow 2S = 2 + 2 + 2 + \dots \\ &\Rightarrow 2S = (1+1) + (1+1) + (1+1) + \dots \\ &\Rightarrow 2S = 1 + 1 + 1 + \dots \\ &\Rightarrow 2S=S \\ &\Rightarrow S = 0 \end{align}$$

Typically the extra conditions involve requiring all but a finite number of the terms to be $0$ ("almost all" in mathematical shorthand) or convergence conditions to make sure that the sum has a limiting value.

This question was asked on January 22, 2020, when I was in my senior year of high school. My questioning was very poor 😅. This is incomparable to someone like Peter Scholze who already known spectral sequences in high school 🙃。