Algebraic Topology I: 对教材跟概念的一些论述
关键词:Homotopy, Homology, Groupoid, Foundamental Group, Van Kampen Theorem, Covering Space, Covering Projection, Fibration with unique path lifting, Cofibration.
Tammo tom Dieck 在他的代数拓扑教材中写了非常漂亮的前言,在点出代数拓扑精髓的同时还包含一些形而上学的哲思,并且简略地介绍了代数拓扑里面的两个核心词汇,同伦(homotopy) 跟同调 (homology)。我简要地部分翻译如下:
代数拓扑是连续数学跟离散数学交相辉映的学科。在连续数学里面,我们用拓扑空间和连续映射这样普遍的形式语言将其公理化。而离散数学则是被我们用来表达代数和组合概念的。在数学语言中,我们用实数来概念化连续形式,但我们建立实数时却是要用到整数。下面举个例子,我们直觉地认为时间是一个连续的没有间断的流动过程,是由一系列不停止的瞬间后继构成的。但在实践中,我们却使用被定义为有周期性的离散模型工具跟自然过程。同样地,我们意识到空间是一个连续体,但我们却用离散的集合形式来表达它。因此,时间跟空间具有拓扑的本质,但代数拓扑允许它们同样具有代数的性质。
古典的代数拓扑主要由构建和使用从拓扑空间的范畴到群这个代数范畴的函子组成。但我们也可以假定整体定性的几何本身具有代数性质。于是这里便有了两种研究代数拓扑的重要思想——同调和同伦。
被庞加莱构造出来的同调概念毫无疑问是数学中最具有独创性和影响力的工具之一。按照同调这基础概念,我们从已经给出组合数据的几何物体出发(一般是具有给定单形(simplicial complex)的空间),用被这些信息决定的核(kernel)与象(image)跟线性映射来产生同调群。
在本书中,关于奇异同调(singular homology)、同调、同调代数(homological algebra)、胞腔同调(cellular homology)的章节组成了对同调理论的介绍,这些章节需要一起阅读,从这便可以看出来对于这些复杂的内容没有简单的直觉解释。
.......
......同伦理论表现了拓扑空间本身被隐藏起来的代数结构,这在对基本群(foundamental group)跟叠覆空间(covering space)的介绍中是很清楚的。纤维化(fibration)跟上纤维化(cofibration)这两个第一眼看上去便很技术化的概念,是用来揭示任何连续映射本身便可以产生像核(kernel)跟余核(cokernel)差不多的结构。
Spanier 也是在他的书最前面一部分内容里面解释了代数拓扑学科的特点,他说他写的这本名为 Algebraic Topology 的教科书本来是要被称为 Functorial Topology 的。因为这个学科本身就是在研究一个个从拓扑空间到某个代数结构的函子。从某种意义上来说,这个学科其实一直在对空间分类。这个会在后面的学习过程中有更深入的体会。
相比于 Hatcher 写的代数拓扑教材,我更偏向以上两本书跟 May 写的教材,这很大程度上就是因为后面这三本书的讲法更符合代数拓扑学科的精神跟气质。而 Hatcher 的书本身便是在后头才介绍和使用范畴的语言,前面的内容基本都是在介绍几何对象的概念。的确那本书他写得很直观,想比于后面那三个人的书确实比较好读,但由于个人品味,我认为代数拓扑作为一个成功公理化的学科,它应该具有代数一样的整洁性,没必要用什么几何直观去拖沓了它。这种公理化的优势从最开始 Eilenberg 跟 Steenrod 写的 Foundations of Algebraic Topology 里面就可以看出来。不过确实,阅读这种代数化色彩浓重的教科书难度很大,需要的前置知识会很多。
May 跟 tom Dieck 写的代数拓扑的教科书还有一个魅力就是,他们自由地使用泛性质(universal property),比如 May 在证明一个 cofibration 诱导出来的空间到 adjunction 的映射也是 cofibration 的时候就只有一张图,但是这图里面的信息却是非常丰富的,这里的证明主要就是用到下图中$B\cup_{g}X$作为 pushout 的 universal property。
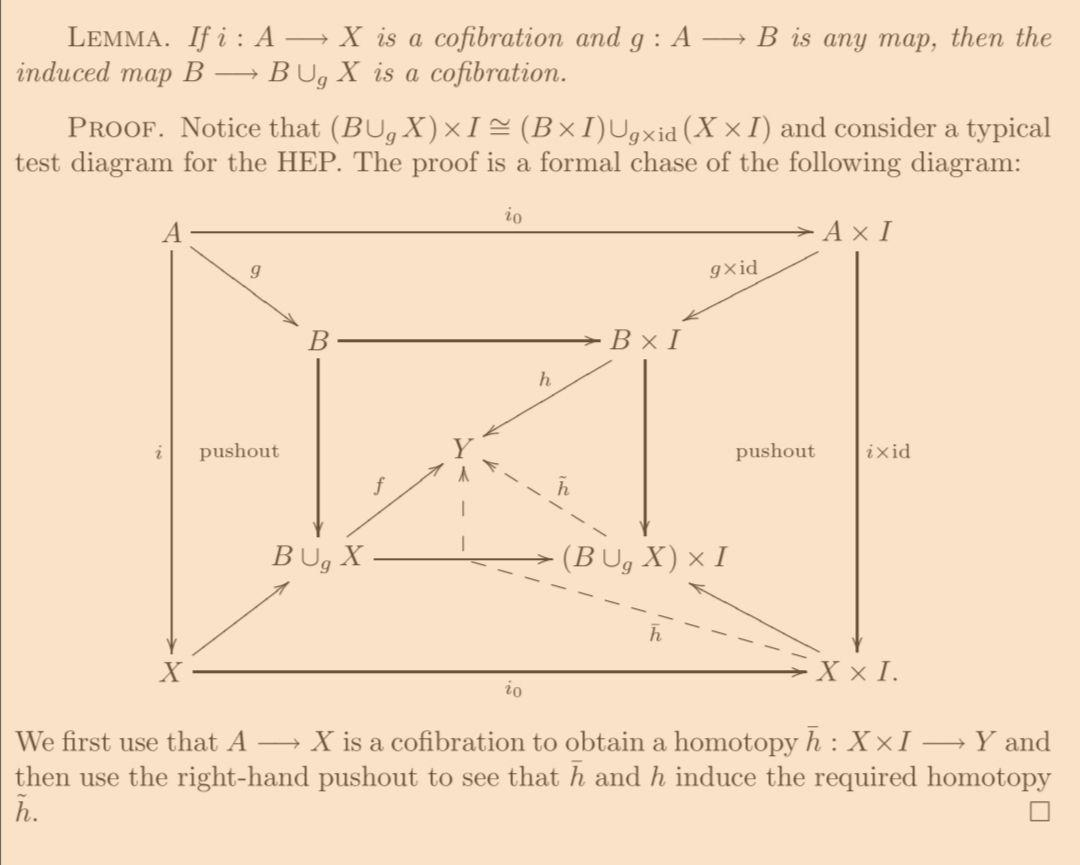 May
May
这就是图的优势,清晰明了,而这样的图你是很难在 Hatcher 的书上看到的,里面大多数情况都是冗长的论述,看证明的时候往往看到一半就忘了前面的(事实上所有代数拓扑教材都很难避免这一点)。
这里要说一下,在 Spanier 或 Switzer 写的代数拓扑教材里面是找不到 pushout 这个词的,我想可能是那时候还没有总结出来。因此他们在处理 Mapping Cylinder 的时候有点繁琐,不如 May 跟 tom Dieck 轻便。而 Rotman 的代数拓扑教材在介绍了 Mapping Cylinder 之后就没有什么后续了。
Rotman 的代数拓扑教材虽然也是有代数化色彩,但是他对有些论题的处理太简单了,不够深入,比如对 Fibration 跟 Cofibration 的论述。同时按照他写书的一贯特色,在有些论题上他写得很拖沓,有些本可以很简明的定理,他却证明地很繁琐,比如证明$H_{n}(X)\cong\oplus_{i}H_{n}(X_{i})$($H_{n}$为 同调函子, $X_{i}$为$X$的路径连通分支)。
其实 Rotman 的那本教材很大程度上是参考 Spanier 的,里面大多数的证明都是来自Spanier,不过 Rotman 那本书有一个优点就是,他给了很多 Spanier 的书上只以结论形式出现而不加证明的一些补充,比如对于 path connected 和 locally path connected 的论述。
很多人不喜欢 Spanier 的书,觉得这本书是写给机器的,而不是人类的,而且这本书第一次出版于 1966 ,他们认为这在今天很可能过时了。我根据我自己的阅读体验来为此说几句话。
首先 Spanier 这本书中浓重的时代色彩是避免不了的,这主要就体现在对一些证明的复杂论述上,里面有很多的定理跟证明是冗长的,一些构造比如用紧生成的拓扑构造出一个空间的路径空间,然后论证在某种条件下原空间是该路径空间的商空间,这种构造是极其复杂的。
而且要注意,在那本书里面一些应用是不在正文里面出现的,比如代数基本定理,它是一道习题。同时 Van Kampen 理论也是以习题形式出现,而且还仅仅是在 simplicial complex 领域内。这是很明显的时代局限,因为 Van Kampen 理论涉及的是 pushout 的保持,而上面说了 Spanier 跟Switzer 的书中根本没出现 pushout 这个词。从这个角度来讲这本书是不适合现在阅读的。对于Van Kampen 很现代的论述可以看 tom Dieck 的或者 May 的,他们写得都很好,不过 May 把它推广到了很深的程度,把 pushout 替换成了 colimit ,而 tom Dieck 则是在另一种角度推广的,他把这个理论推广成了Groupoid 范畴之间的 pushout 的保持(这其实也包含在了 May 的书上)。事实上,这两本书中的证明基本上是互通的,而关于 groupoid 的结论,两个应该互补,tom Dieck 上应该加上任意覆盖,May 的书上应该去掉路径连通的条件,这不影响证明。后面对于基本群上的证明,无穷覆盖下会比有限覆盖下麻烦,需要把有限覆盖下的情况作为引理才能证明无限覆盖下的情况,具体可以看 May 的,里面用到两个 colimit 可以交换的性质。
 Tammo Tom Dieck
Tammo Tom Dieck
但是我真的要说一句, Spanier 写的这本书证明非常清晰,尤其是那些复杂的构造,他写得很清楚。并且里面尽可能地用一般的方法将概念普遍化,他不是像 tom Dieck 那样比如讲 covering projection 的时候,直接先定义 fiber bundle,然后说 covering space 是具有离散 fiber 的 fiber bundle,而是一步步地告诉你为什么要这么推广,为什么要更普遍的概念。在 covering space 那个章节他很大部分都在讲 fibration with unique path lifting ,他最开始就花了大篇幅证明我们的 covering projection 其实就是一个 fibration with unique path lifting,之后所有对这个特殊的 fibration 的结论都能套到 covering space 身上。首先这种普遍化可以简化很多证明,covering projection 的条件是很强的,要用它证明一些定理虽然可以办到但是会受到一些不必要的性质的影响。而用 fibration 证明的时候,我们一般只需要它的 homotopy lifting 性质。另外我们为什么需要 fibration 这个概念?他告诉我们,因为 covering projection 不在 product(可无限乘积) 跟 composition 下封闭,而不管有没有 unique path lifting 这条性质的 fibration 都是对它们封闭的。由此我们可以形成一种由 fibration 这个 object 构成的范畴,这是 covering projection 办不到的。
另外,有时候由于 covering projection 的条件太强了,它会掩饰掉一些更加本质的东西。比如当我们判断$p:E\to X$是不是同胚的时候,假如$p$是一个 covering projection ,那么当$E$是路径连通的时候,我们有$p$为同胚映射当且仅当$p_{*}\pi_{1}(E,e)=\pi_{1}(X,x)$。
“$\Leftarrow$” :这是因为$E$是路径连通的就默认了$X$也是路径连通的,因此$\left|p^{-1}(x)\right|=[\pi_{1}(X,x):p_{*}\pi_{1}(E,e)]=1$(这个定理在 Spanier 的 P73,利用 oribit-stabilizer theorem),于是$p$为双射。再由于 covering projection 是局部同胚的,因此是 open 的,所以$p$是同胚的。
而在 fibration with unique path lifting 的条件下,我们得要求$X$是 connected and locally path connnected,$E$是 path connnected ,这样在知道$p$为双射的同时我们能够把$1_{X}$提升到$E$上,即存在$s:X\rightarrow E$使$p\circ s=1_{X}$成立。
这是一个定理,假如$p:(E,e)\rightarrow (X,x)$是一个 fibration with unique path lifting,$(Y,y)$是 connected and locally path connnected,并且$f:(Y,y)\to (X,x)$具有性质$f_{*}\pi_{1}(Y,y)\subset p_{*}\pi_{1}(E,e)$,那么存在$g:(Y,y)\to(E,e)$使$p\circ g=f$成立。
这里 covering projection 就把 lifting 性质给隐藏掉了。
从这种传统的角度入手讲解 fibration 跟May 或者 tom Dieck 那种全篇用 universal property 来讲解真的是两种完全不同的体验。我觉得 Spanier 写出了过去代数拓扑那雄浑的气质,毕竟在那个时候代数拓扑是最为成功的数学领域,数学家在由来已久的空间分类上取得了巨大的成功。我或多或少能从他的前言里面体会到他作为代数拓扑学家对这个学科的成功而感到自豪。从这个角度来看我觉得Spanier 的书很像 Robin Hartshorne 写的 Algebraic Geometry,他从最开始的Variety讲起,一步步地进入 Scheme ,在古老跟现代的交织中论述概念。
而 tom Dieck 跟 May 的教材则更偏向于现代的风格,他们自由地使用范畴论语言,而这就又给人一种很轻灵的感觉,好像代数拓扑它从过去的语言体系中解放了出来,变得轻快起来,不再像以前那样厚重得甚至给人压抑感。他们把信息都蕴含在图(序列)中,里面很多细节都是需要读者自己去摸索探寻的,往往你会惊讶一张图里面竟然蕴含了这么多的信息。这或许可以跟刘青的 Algebraic Geometry and Arithmetic Curves 或者 Vakil 的书相比,他们相较于 Hartshorne 是单刀直入迅速地进入 Scheme。
此外,Spanier 有时候写的一些补充是很简略的,而例子也是直接告诉你该案例不符合或符合什么什么,而不给你细节的论证(里面有些例子的性质我自己推不出来,这时候可以参考Rotman的),但他的正文确实写得不错,详细并且逻辑性强。
tom Dieck 跟 Spanier 的两本教科书都是在最前面的时候阐述了代数拓扑的原则,而 Spanier 更是在第一节关于范畴论的内容里面讲了很多例子。最简单的我们有所谓的$\pi_{0}$函子,它是从拓扑空间到该拓扑空间的路径连通分支集合,是一个从$Top\to Set$的函子,利用这个函子我们做到分辨$R$跟$R^{2}$,因为去除$R$上的$0$我们得到两个路径连通分支,而去除$R^{2}$上的一个点,我们只能得到一个路径连通分支。因此$R$跟$R^{2}$不是同胚的。这就在某种程度上完成了对这两个空间的分类。
而有时候在某个函子下我们的目标空间还是得不到区分,这样我们就需要更加细致的函子。在上面的例子里面$\pi_{0}$函子是非常简单的,因为集合本身不带有任何代数结构。随后的一些函子所面对的结构都是有代数性质的,比如交换群。在简单函子下不能得到区分的空间,在复杂的函子下便可能得到了区分。比如$\pi_{1}(S^{1})\cong\mathbb Z$而$\pi_{1}(S^{n})=0, n\geq 2$。
同时,有一些从拓扑空间到代数范畴的函子是“无用”的,因为判别两个拓扑空间同胚(或者同伦)跟判别对应的两个代数对象同构一样复杂。Spanier 对这个情况也举了一个例子,函子$C:Top\to Ring, C(X)=Hom(X,R)$为该空间到实数上的连续映射,这个集合带上实数上的加法跟乘法后具有环的结构。两个 Compact Hausdorff Space 同胚,当且仅当诱导出来的两个环同构 ( 可以参考 Dugundji 写的拓扑学 P289)。在这个时候,我们判别这两种等价都是很困难的。
微分拓扑所做的工作原则上跟代数拓扑是一样的,它们也是在分类空间,不过它们的研究对象是流形而不是一般空间,分类的标准是流形上的 Chart 而不是同伦。
上面的这些内容都是隶属于最基本的同伦论,tom Dieck书中前200页对同伦论的阐述是非常老练的,他写的这本教科书在该简洁的时候非常简洁,同时里面内容非常丰富,概念出现的频率很高,有时候概念是成批一起出现在一个段落里面的。
我觉得,没有事先接触过代数拓扑或者同伦论的人很难在阅读中体会到那种优点。也因为这个,出于对同伦论的不熟悉,在阅读 tom Dieck 的书时,我没有像阅读 Spanier 那样顺畅。从某种意义上我或许可以这么说,Spanier 的书是在教导学生古典代数拓扑,而 tom Dieck 更像是向学生展示一个现代代数拓扑学家是怎么证明这些古典代数拓扑命题的。在细节的地方,他处理得很简单,很多微小的性质他都是直接告诉你的,而不加以证明。但是里面很多的处理方法是我在 Spanier 的书中看不到的。
tom Dieck 好像特别偏好于构建范畴,他经常把一些定理放置在自己专门构建出来的范畴里面论述,比如在分类 covering space 的时候,他就是这么干的。还有,他在foundamental group 的章节末尾处介绍了 2-category,Maclane的书中一道习题就是利用 2-category 证明了 topological group 的 foundamental group 是交换的。因此 Spnier 里面繁琐复杂的论述到了 tom Dieck 这里就变得很简洁,这样更能让人体会到同伦论或者范畴论的强大力量。
此外,不管 Spanier 还是 tom Dieck,我觉得他们的书里面虽然有不少例子,但是有些例子他们确实写得过于简略,而 Hatcher 的书里面,例子往往都是有详细论述的,因此看不懂上面两本书的例子的时候,去翻翻 Hatcher 的书,或许可以有所收获。
之后阅读这三本代数拓扑,有收获的话我会继续更新。
此外代数拓扑还有很多其他的经典教材,比如 Lectures on Algebraic Topology by Albrecht Dold ,这本书的特点是很少讲同伦,整本书几乎都是在讲同调,里面同调理论的内容讲得很深入,比如讲到了 Cech Cohomology ,对同调理论在流形上的应用有很精彩的论述。这本书的叙述特点有点像 Tammo tom Dieck的,或者说 Tammo tom Dieck 像他的,毕竟 Dold 是 Tammo tom Dieck 博士导师。Dold 他对定理的证明也是很简洁... 里面很多 gap 要你自己补充。Dold 本身就是一个厉害的代数拓扑学家,他的成果比如 Dold-Kan correspondence,Dold-Thom theorem。我第一次发现这本书是在 Maclane 写的 Homology 里面,他说 Dold 教授修正了本书在 Homology classification theorem 里面的分裂构造,然后 Maclane 在新的版次里面引用了这本代数拓扑对该定理的证明。
Lecture Notes in Algebraic Topology by Paul Kirk James F. Davis 这本书的重点是后面半本书的谱序列,作者在每个章节后面都列出了补充的 project ,这个需要读者自己额外去查找资料。这本书不适合第一次阅读,它本身就是作为第二次上代数拓扑课程的教材,因此很多概念是默认读者已经知道的,比如 CW-complex。当然,假如你打算看 A User’s Guide to Spectral Sequences by John McCleary 的话,那这本书就显得多余了,或许它能提供其他论题的新思路,不过我看它在传统论题的处理上,比如 obstruction theory 都是要求学生去看看其他书籍,obstruction theory 要求的就是 Spanier 的书。
Algebraic Topology from a Homotopical Viewpoint by Marcelo Aguilar, Samuel Gitler, Carlos Prieto, S.B. Sontz 这本书也是写得很有特点,全篇基本都是讲同伦的,只有少数因为需要才讲了一点同调,而且这本书经过了 Dold 教授的阅览跟修订... 真的是,这本书跟 Dold 的那本书形成了补充,一个讲同调,一个讲同伦。这本书后面的论题很深入,我不太了解里面的具体内容,它讲到了 K-theory,还有Generalized Cohomology Theories 跟 Brown Representability Theorem ,而 Brown Representability Theorem 我现在只在 Categories and Sheaves by Masaki Kashiwara, Pierre 这本书里面见过。该书的目录具体可以看下图

当然还有很多其他的讲代数拓扑跟同伦论的经典教材,比如 Switzer,Whitehead,Selick 等等,就不一一细讲了,毕竟很多我也没仔细看过。
Reference
- Algebraic Topology by Spanier
- A Concise Course in Algebraic Topology by May
- Algebraic Topology by Tammo tom Dieck
原文地址: https://zhuanlan.zhihu.com/p/260821664
Tammo tom Dieck代数拓扑教材的下载地址,站内见Tammo Tom Dieck代数拓扑教材。
There is no comment, let's add the first one.