My question:

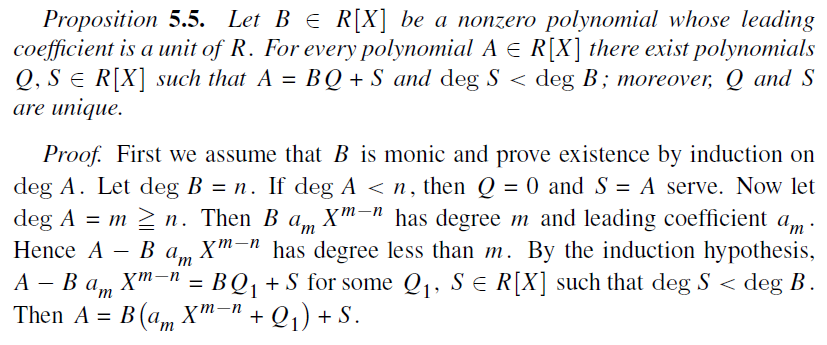
I fail to understand how the induction step is carried out in this proof. Can anyone help? Thanks!

Answer: Fix $n = deg B$. They are proving the statement by inducion on $m = deg A$. The base case is $m < n$. If $m \geq n$, then they find another polynomial $A'$, in this case $A' = A - B a_m X^{m - n}$, which has degree smaller than $m$, so we can deal with it by induction hypothesis. The quotient-and-remainder representation of $A'$ is used to find that of $A$.

I suppose there are two things that you may find bothering, and why you didn't recognize the induction. First, that the base case is not just one case but a bunch of them. Notice that here this was fundamental: the induction step in the proof only works for $m\geq n$. Also, notice that in this case proving it for $m=1$ is not less work that proving it for $m<n$: it was a one-line proof for all of these cases.

The second thing you may find bothering is that we are not only using the induction hypothesis for $m−1$, but for any polynomial with degree strictly smaller than $m$. This is called complete or strong induction: where in the induction step, you use the hypothesis that the statement is true up to $m−1$, and not just for $m−1$. On the wikipedia page for induction it's explained well.