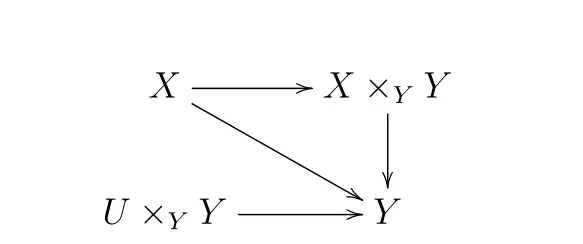
My question: Let $X,Y$ be schemes. Let $X\rightarrow Y,X\rightarrow X, Y\rightarrow Y$ be morphisms of schemes. Why the morphism $U\times_{X}X\rightarrow U\times_{Y}Y$ is the base change of $X\rightarrow X\times_{Y}Y$ by $U\times_{Y}Y\rightarrow Y$?

Here is the diagram I try, where the triangle is commutative. But I found that $(U\times_{Y}Y)\times_{Y}(X\times_{Y}Y)=U\times_{Y}X\times_{Y}Y=U\times_{Y}X$, i.e. I can not obtain the desired $U\times_{X}X$. What mistakes do I make?

Here is the context in question, from Xinwen Zhu's paper Affine Grassmannians and the geometric Satake in mixed characteristic (arXiv link):

Lemma A.2. For any étale morphism of algebraic spaces $X\to Y$, the relative Frobenius morphism $X\to X\times_{Y,\sigma_Y}Y$ induced by $\sigma_X$ is an isomorphism.

Proof. We first assume that $X$ is a scheme. Then $X\to X\times_{Y,\sigma_Y}Y$ a schematic radical étale surjective map, and therefore is an isomorphism by \cite[Theorem 17.9.1]{EGA4-4}.

For general $X$, choose an étale cover $U\to X$ by a scheme $U$. Then we have $U\to U\times_{X,\sigma_X}X\to U\times_{Y,\sigma_Y}Y$, with the first map and the composition map being isomorphisms. Therefore, the second map is an isomorphism as well. Note that $U\times_{X,\sigma_X}X\to U\times_{Y,\sigma_Y}Y$ is nothing but the base change of $X\to X\times_{Y,\sigma_Y}Y$ along the étale cover $U\times_{Y,\sigma_Y}Y\to Y$. Therefore, $X\to X\times_{Y,\sigma_Y}Y$ is also an isomorphism.

Answer: The diagrams are a bit more complicated than you're using here. First, we have a base change diagram defining $X\times_{Y,\sigma_Y} Y$ as follows:

$$\begin{CD} X\times_{Y,\sigma_Y} Y @>>> Y\\ @VVV @VV{\sigma_Y}V \\ X @>>> Y \end{CD}$$

The morphism $X\to X\times_{Y,\sigma_Y} Y$ is induced by the identity morphism $X\to X$, the morphism $X\to Y$, and the universal property of the fiber product.

The diagram defining $U\times_{Y,\sigma_Y} Y$ is as follows:

$$\begin{CD} U\times_{Y,\sigma_Y}Y @>>> X\times_{Y,\sigma_Y} Y @>>> Y\\ @VVV @VVV @VV{\sigma_Y}V \\ U @>>> X @>>> Y \end{CD}$$

Now base change the entire first diagram plus the induced morphism $X\to X\times_{Y,\sigma_Y} Y$ by the map $U\times_{Y,\sigma_Y} Y\to Y$ to get the claimed map.

The previous article What is base change map ? is indeed inspired by this question.