一般编辑器分为Markdown编辑器和富文本编辑器两种，而弦圈目前所用编辑器为富文本编辑器，暂不支持Markdown编辑器。个人认为富文本编辑器对新手更为友好。

富文本编辑器用法跟Word大致相同，基本功能不再赘述。在本文中，我们将介绍一下弦圈编写文本所用编辑器的一些特殊功能。这些功能包括插入词条、添加参考文献、引用文献。

插入词条

插入词条指的是在文本中插入一条圈子百科中词条的链接。主要用于文本中一些难懂且解释需要篇幅的术语。在编辑器中直接点击下图按钮即可进行输入。

点击后会弹出对话框，根据提示把带星号的项填好，点击下面的“插入”按钮即可。

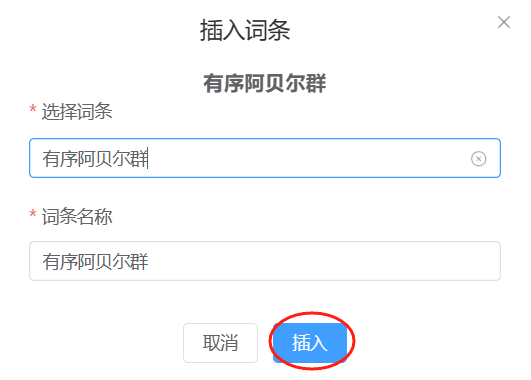
插入词条后，编辑器中结果如下：

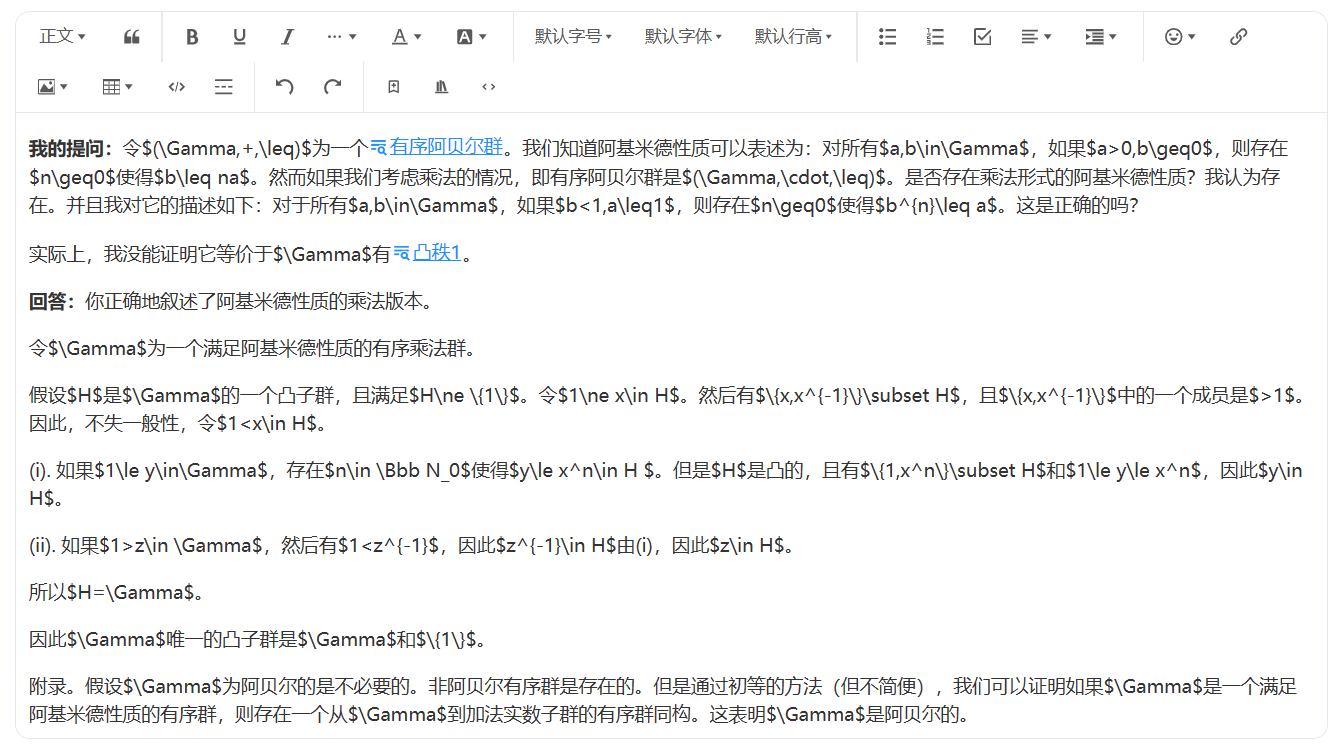
发布文章后的效果如下，点击该链接会弹出该术语在圈子百科中的相应解释，非常方便查找相关术语的意思，不用多个页面互相切换：

令$(\Gamma,+,\leq)$为一个有序阿贝尔群。

添加参考文献

添加参考文献指的是在文章的中插入论文格式的参考文献。该功能用于帮助用户生成美化过的、条理性强的、符合论文格式要求的参考文献。在编辑器中直接点击下图按钮即可进行输入。

点击后会弹出输入框如下图，根据提示将带星号的项填好，然后点击下方蓝色“确定”按钮即可。

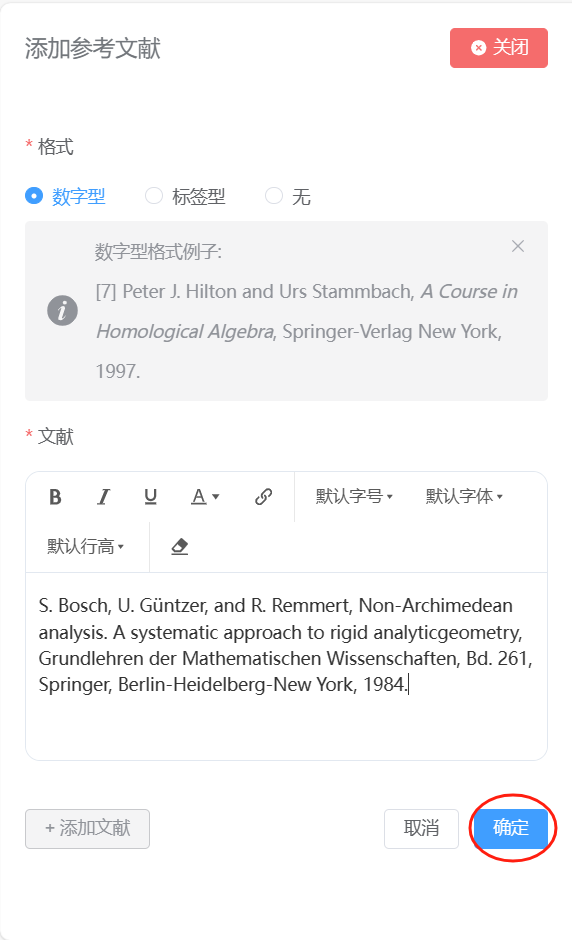
添加参考文献后，编译器的效果如下：

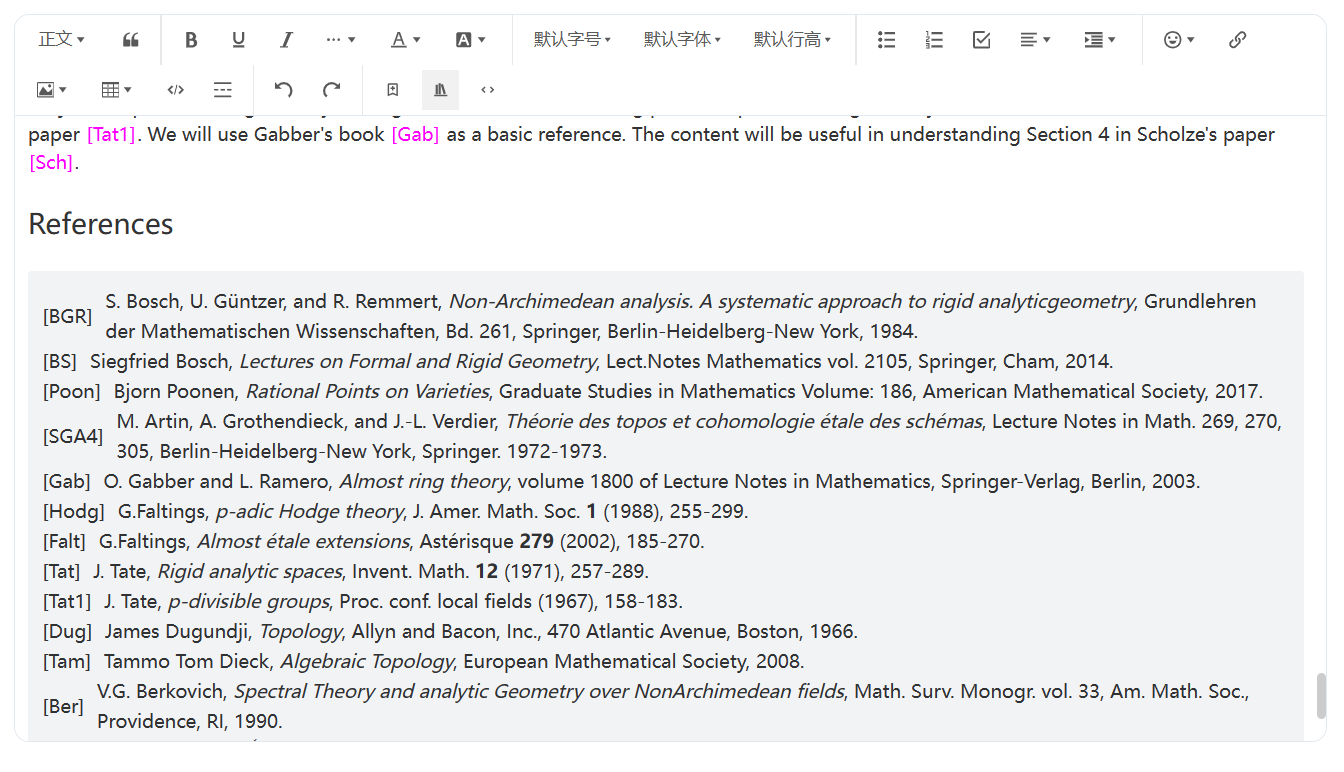
发布文章后生成的效果如下：

引用文献

当你在文章中添加完参考文献后，就可以使用“引用文献”进行引用了。在编辑器中直接点击下图按钮即可进行输入。

点击后会弹出对话框，根据提示将带红色星号的项填好，然后点击下方蓝色“确定”按钮即可。

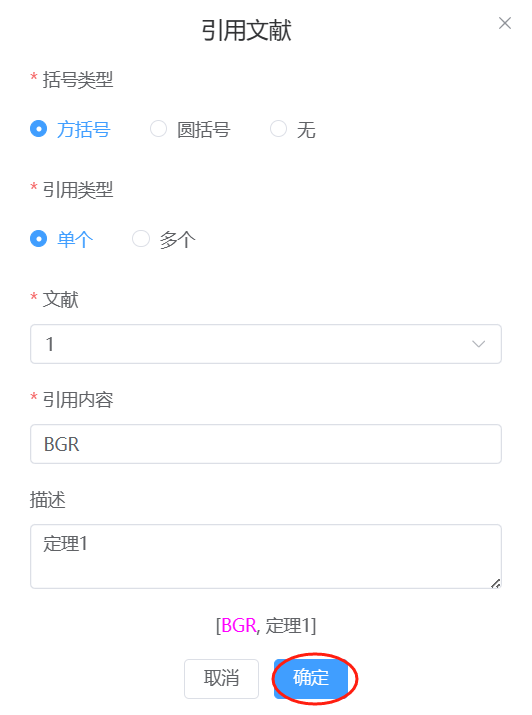
引用文献后，编辑器中的效果如下：

发布文章后生成的效果如下，引用为一个粉色链接，点击链接后页面会跳到相应的参考书目上：

[BGR, 定理1]

至此关于弦圈编译器的功能介绍完毕，祝您使用愉快！