存在最长的10个诸侯国,最长的将近两千年,几乎横跨半个华夏史
中国历史悠久,上下约5000余年。从夏商开始就出现过许许多多的诸侯国。那么,在这些诸侯国中,国祚最长的是哪一个国家呢?
很多人可能觉得是卫国,因为卫国是战国时期最后一个灭亡的诸侯国。那么,卫国真的就是中国历史上存在最长的诸侯国吗?
其实不是,还有很多的诸侯国存在的时间都比卫国长得多。这些诸侯国一般人都鲜为人知。他们这些诸侯国中国祚最长的将近两千年。
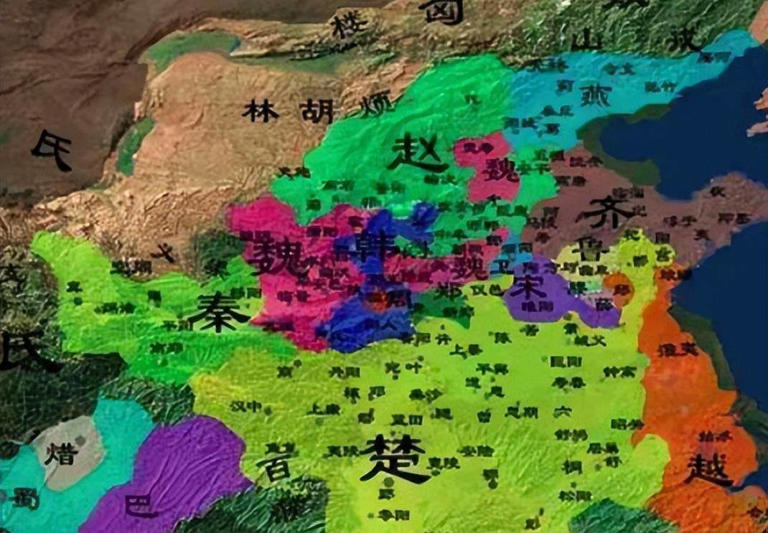
10、楚国
存在时间:公元前1042年——公元前223年,国祚819年。
楚国,又称荆、荆楚 ,是先秦时期位于长江流域的诸侯国,国君为芈姓、熊氏。公元前1042年,封楚人首领熊绎为子爵,建立楚国。公元前223年,秦军攻破楚都寿春,楚国正式灭亡。
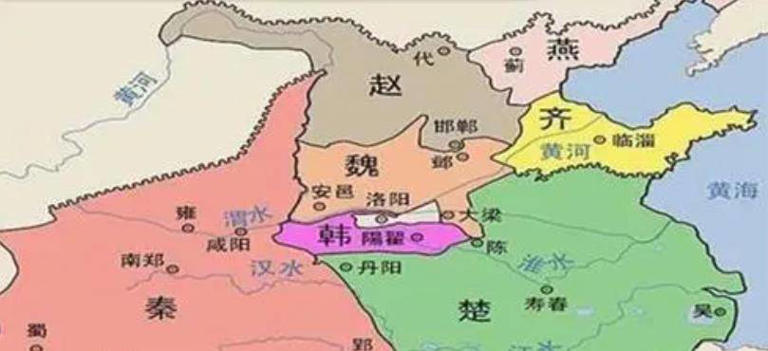
9、燕国
存在时间:公元前1044年——公元前222年,国祚822年。
燕国是周朝的周王族诸侯国之一,始祖是周文王庶长子召公。公元前1044年,周武王灭商后,封其弟姬奭于燕地,是为燕召公。公元前7世纪,燕国向冀北、辽西一带扩张,吞并蓟国后,建都蓟(今北京市)。公元前222年,秦王嬴政派王贲率军进攻辽东,虏燕王喜,燕国灭亡。
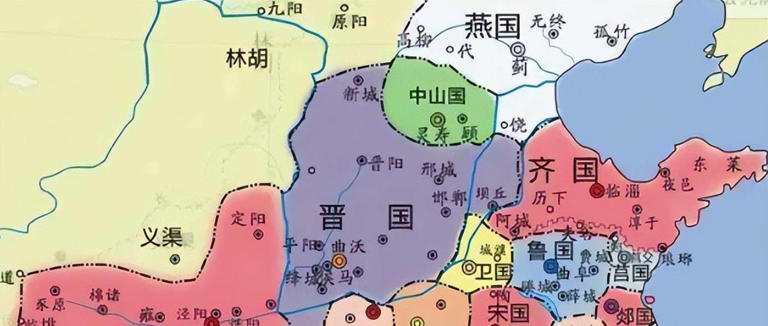
8、齐国
存在时间:公元前1046年——公元前221年,国祚825年。
齐国是中国历史上从西周到春秋战国时期的一个诸侯国,被周天子封为侯爵,分为姜齐和田齐两个时代,疆域位于现今山东省大部,河北省南部。始封君为太公望(姜子牙)。公元前221年,齐王建向秦王政投降,齐国覆灭。
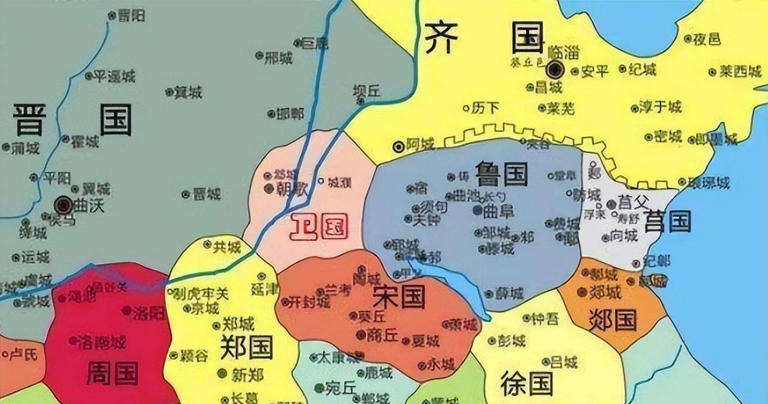
7、卫国
存在时间:公元前1117年——公元前209年,国祚908年。
卫国周朝的姬姓诸侯国,第一代国君康叔封,传41君,是众多姬姓诸侯国中最后灭亡的国家。卫国是存在时间最长的周代诸侯国。
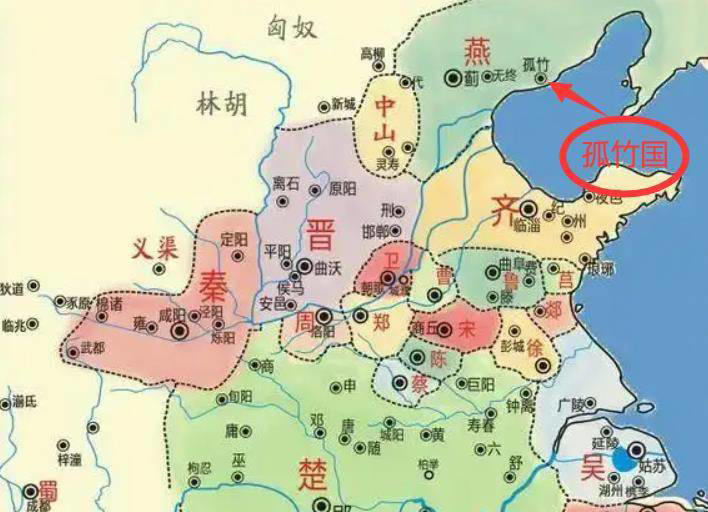
6、孤竹国
存在时间:公元前1600年——公元前664年,国祚936年。
孤竹国诞生于约公元前1600年前商朝初期,是冀东辽西地区出现最早的国家。商朝初年,封同宗是血亲墨姓为君的国度。孤竹先人为先商部族墨氏一支,国君子姓墨氏。公元前664年,齐桓公为救燕出兵伐山戎,灭亡孤竹国。
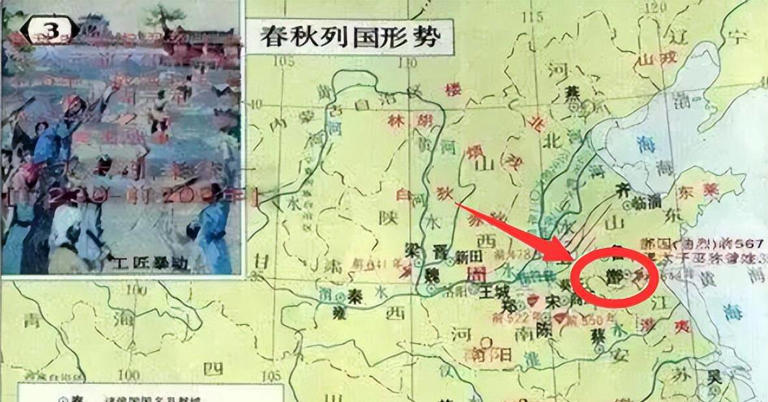
5、叛国
存在时间:公元前1950年——公元前567年,国祚1383年。
蒙国亦作“缯国”,是夏代少康次子曲烈的封国,因始封地名为“鄫”而得国名。蒙国是东方建国较早、比较活跃的诸侯国之一,国君为姒姓。鄫国历夏、商、周三代,于公元前567年,被莒国灭亡。
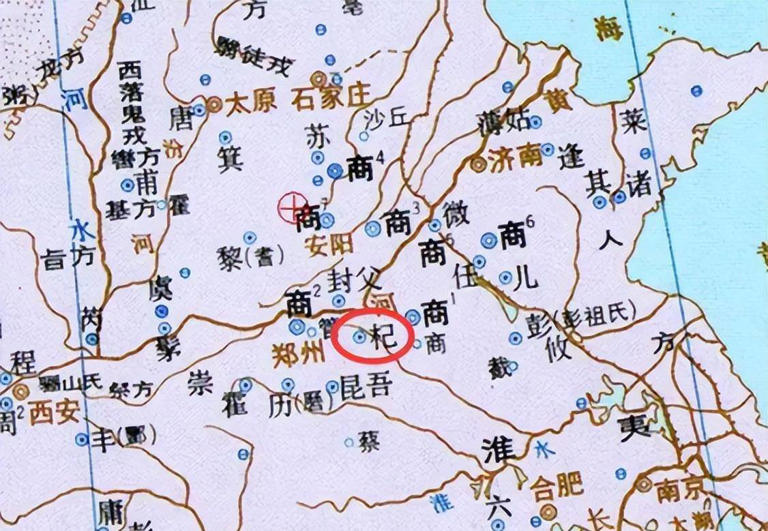
4、杞国
存在时间:公元前2000年——公元前445年,国祚1550年。
杞国,中国历史上自夏代到战国初年的一个诸侯国,约公元前2000年建国,由华夏族所建立,国祚延绵1550多年,国君为姒姓,大禹的直系后裔。公元前445年,齐国亡于楚国。
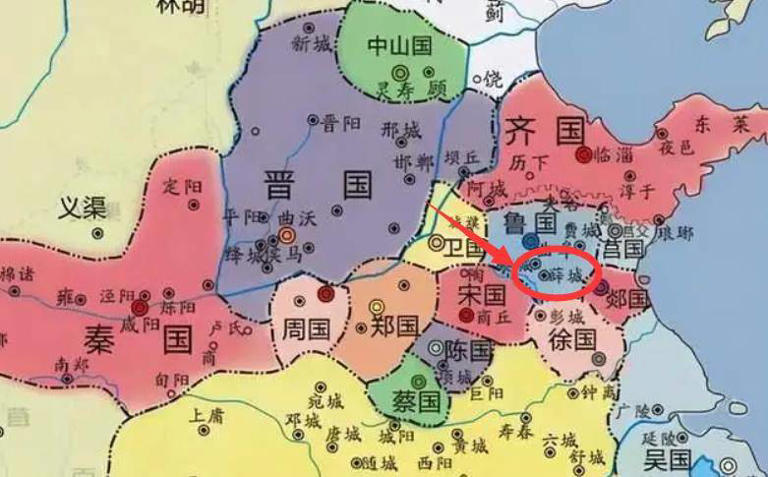
3、薛国
存在时间:公元前2000年——公元前418年,国祚1582年。
薛国,约公元前2000年,夏禹封发明车的奚仲立国,国君任姓,在今山东省滕州市官桥镇和张汪镇之间。传说奚仲是炎帝后裔。公元前418年,齐国灭薛国。
2、徐国
存在时间:公元前2000年——公元前512年,国祚1600年。
徐国,约公元前2000年,夏禹时封治水功臣伯益子若木建徐国,国君赢姓,都城为徐城(今江苏省宿迁市泗洪县)。公元前512年冬天,吴王派孙武、伍子胥灭亡徐国,徐国历四十余君。
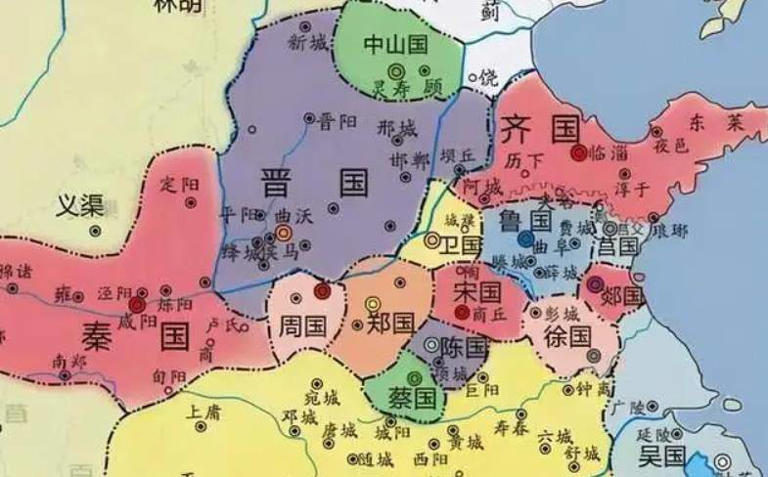
1、越国
存在时间:公元前1950年——公元前111年,国祚1839年。
越国,约公元前1950年的夏朝时期建国。越国处在东南扬州之地,《史记》记载其始祖为夏朝君主少康的庶子无余,是大禹的直系后裔中的一支。越国与杞国、缯国、褒国等皆为大禹后裔子孙所分封。公元前306年,越王无疆攻楚兵败身亡,越国分裂为东越,闽越等国。秦汉时期百越还存在,汉武帝时期,前111年,闽越余部迁徙到了江淮一带居住,彻底消亡。算到楚灭越国,享国时间1644年,算到汉武帝时期,享国时间1839年。
暂无评论,来发布第一条评论吧!