Vue3中的条件渲染(v-if、v-else-if、v-else 以及 v-show)的使用(实例详解)
v-if v-else v-else-if
v-if指令用于条件性地渲染一块内容,这块内容只会在指令的表达式返回truth值的时候被渲染。
<script setup>
const have = ref(true)
</script>
<template>
<div id="app">
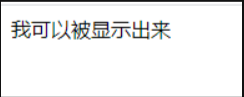
<div v-if = "have">我可以被显示出来</div>
</div>
</template>当have的值为true时,div块被显示。
而当have为false
const have = ref(false)页面无显示,且具有v-if = “have”的div块不存在在html结构中。
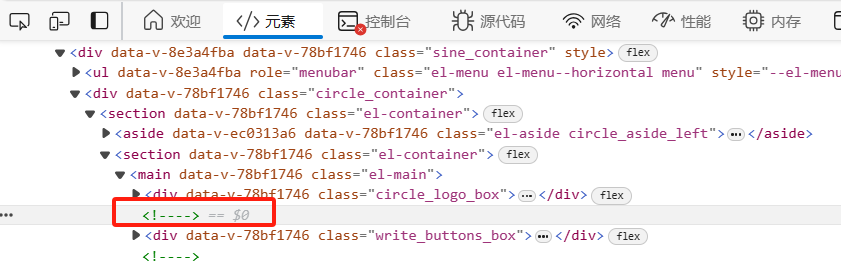
也可以用v-else添加一个“else模块”,和js的语法相同,当if条件不成立,则显示else模块内容。
在vue2.1.0新增的v-else-if,更是可以与上面两个共同使用,但是v-else和v-else-if都必须紧跟在v-if的后面使用(v-else-if可以跟在v-else-if后面)
例子:
<script setup>
const type = ref("哎哎哎")
</script>
<template>
<div id="app">
<div v-if="type==='A' ">A</div>
<div v-else-if="type=='B'">B</div>
<div v-else-if="type=='C'">C</div>
<div v-else-if="type=='D'">D</div>
<div v-else>not A/B/C/D</div>
</div>
</template>执行结果:

这里其他的div在html结构中已不存在。

在<template>元素上使用v-if条件渲染分组
因为v-if是一个指令,所以必须将它添加到一个元素上,但是如果想切换多个元素呢???此时就可以把一个< template>元素当不可见的包裹元素,并在上面使用v-if,最终的渲染结果将不包含< template>元素。
例子:
<script setup>
const ok = ref(true)
</script>
<template>
<div id="app">
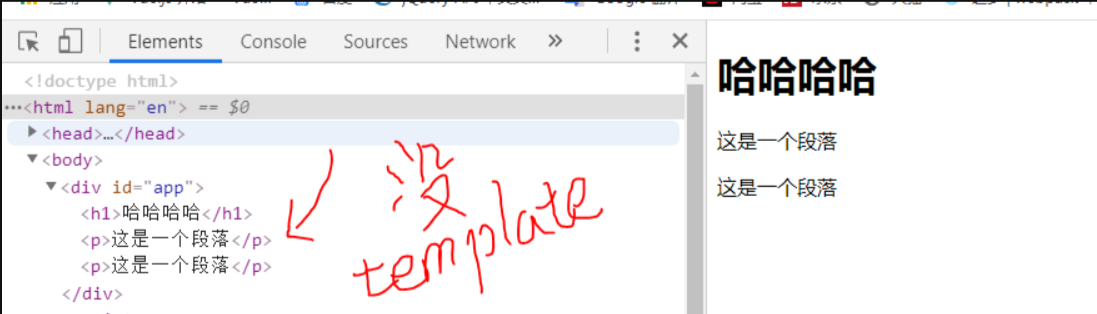
<template v-if="ok">
<h1>哈哈哈哈</h1>
<p>这是一个段落</p>
<p>这是一个段落</p>
</template>
</div>
</template>运行结果:
v-show
v-show是另一个用于根据条件展示元素的选项,,用法和v-if大致相同
<h1 v-show="ok">hello</h1>不同的是带有v-show的元素时钟会被渲染并且保留在dom中,v-show只是简单的切换原色的css属性display
(注意)v-show不支持template元素,也不支持v-else
例子:
<script setup>
const ok = ref(false)
</script>
<template>
<div id="app">
<div v-show="ok">hhhhhhhhhhh</div>
</div>
</template>不显示但存在

v-if和v-show的区别
v-if
- 是真正的条件渲染,因为它会确保在切换过程中事件内的**事件监听器和子组件适当得被销毁和重建。
- 是有惰性的:如果在初始渲染的时候事件为假,则什么也不做,直到条件第一次变为真的时候,才会开始渲染条件块
v-show
相比v-show就简单的多,不管初始条件是什么,元素始终都会被渲染,而且只是简单地基于css进行切换。
两者的使用
一般来说,v-if有更高的切换开销,而v-show有更高的初始渲染开销,因此,如果需要非常频繁地切换,则用v-show更好一些;如果运行的条件很少改变,则用v-if更好。
暂无评论,来发布第一条评论吧!

