预层
令$X$为一个拓扑空间。
一个$X$上的(集合)预层$A$是一个从$X$的开集和包含映射的范畴到集合范畴的逆变函子。
分享
举报
- 一个$X$上的集合预层是一个法则,对每个开集$U \subset X$都有一个集合$\mathcal{F}(U)$与之对应,对每个包含映射$V \subset U$都有一个映射$\rho ^ U_ V : \mathcal{F}(U) \to \mathcal{F}(V)$与之对应,使得$\rho ^ U_ U = \text{id}_{\mathcal{F}(U)}$,并且对任意$W \subset V \subset U$,我们有$\rho ^ U_ W = \rho ^ V_ W \circ \rho ^ U_ V$。
- 一个$X$上集合预层的态射$\varphi : \mathcal{F} \to \mathcal{G}$是一个法则,对每个开集$U \subset X$都有一个函数$\varphi : \mathcal{F}(U) \to \mathcal{G}(U)$与之对应,该函数与限制映射兼容,即对任意开集$V \subset U \subset X$,图
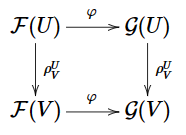 是交换的。
是交换的。
相关内容
本词条暂无相关内容