人类眼睛的秘密:高达5.76亿像素,占用65%脑力,这意味着什么
综述
俗话说,眼睛是心灵的窗口,其实眼睛也是我们大脑处理信息的通道。通过眼睛,纷繁多彩的大千世界得以进入我们的大脑,再经由大脑,为这些进入眼睛的图像赋予更为丰富的意义。
大家都知道,脑力劳动需要消耗许多的能量和氧气,但出乎大家意料的是,大脑的这些耗能有65%都用在了眼睛上面。
实际上,占用65%脑力的眼睛,功能远比你我想象的更为强大。

眼睛的结构
人类的眼睛体积不大,是人体中比较小巧的一个器官,但眼睛虽小,但它其中却蕴含着许多细胞与结构。
从整体来看,眼睛呈一个比较规则的圆球状,位于眼眶内。在眼睛最前端的就是角膜,角膜除了是眼睛收集外界信息的最主要的一个方式外,还对眼睛有着一定的保护作用。
角膜之下,位于眼球壁第二层的便是我们的葡萄膜,也即眼色素,由于这层膜取出后像一个葡萄,呈紫黑色,又圆又软,因此叫葡萄膜。
葡萄膜富含黑色素和血管,血流量大、血流速度缓慢,眼球的血液营养便是由它提供。此外,由于血液里的致病性抗原物质会在葡萄膜中沉淀,因此它与全身性疾病有密切联系。

葡萄膜的前部就是虹膜,也就是我们常说的“黑眼球”,中央有一个小圆孔,即瞳孔。光线便由此进入眼内。
再往里看,就到了视网膜,视网膜在眼睛的最内部,是透明的。由于视网膜中存在着许多可以与大脑进行信息交互的活跃细胞,这便赋予了视网膜的两大功能,即在眼睛中进行物质的代谢和信息的传递。
眼睛的这些“装置”,对于眼睛执行信息成像功能都是不可或缺的,并且它们都相当灵活,可以依据环境变化作出相对应的反应。
眼睛的功能
了解了眼睛的基本结构之外,我们再来看看它的功能。
作为一个视觉器官,眼睛的主要功能自然是成像。在摄取到外界信息之后,眼睛会自动将这些信息转换为图像,再以图像形式传递给大脑,然后我们的大脑就能对这些图像进行“解码”,分析处理之后,大脑再指挥身体的其他器官作出反应。
那么,眼睛是如何完成成像这一步骤的,它的工作原理是什么?

我们知道,人眼的结构是一个凸透镜。因此,眼睛成像的原理与凸透镜成像的原理是相似的,不过眼睛不是一面简单的凸透镜,它的成像系统还要复杂一些。
当光线进入眼睛后,会经过角膜、晶状体等一系列眼部结构的折射和调节,最终在视网膜上形成图像。
这种由实际光线会聚而成的图像被称为实像,而实像区别于虚像的一个重要体现就是实像是倒立的,虚像是正立的。

因此,若根据眼睛成像的原理,我们看见和感受到的应该是一个颠倒的世界。
但事实并不是如此,最终呈现在我们眼中的世界是正立的,而这就要归功于大脑了。
在我们所不知道的地方,大脑已经为我们适应了这种倒立,它将视网膜上形成的缩小的倒立实像进行了生理性的回转,将颠倒的物象纠正了过来,使之与外界现实相符合。
事实上,如果我们把头倒过来看世界的话,要不了几周时间,我们的大脑也可以适应“倒着看世界”。
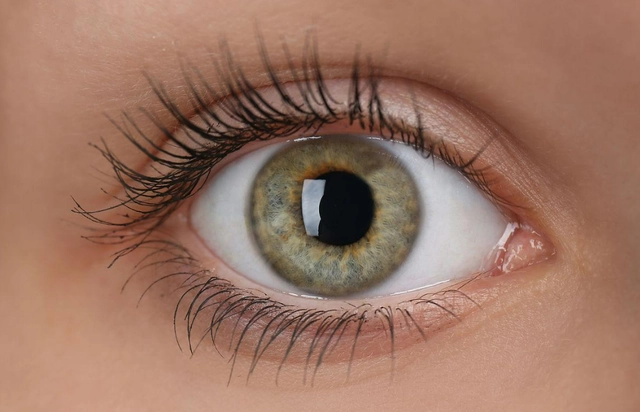
眼睛的像素
眼睛背后的成像原理也给了影像行业启发,后来发明的照相机在某种程度上就是仿照了眼睛的结构:可以调节进光量的瞳孔,被人类仿造成了光圈;能够处理远近物体成像的角膜瓣,被我们制造成了焦段。
那么,同样是人类捕捉世界影像的工具,工作原理也一致,人眼和相机究竟谁的像素更高?
据科学家兼摄影师——罗杰·克拉克(Roger Clark)博士的说法,人眼的数码图像分辨率为5.76亿像素。

而民用相机的像素大都在千万之间,少有突破一亿的。
因此,若根据数据来看,尽管现有的摄像技术已经很高,但是这些设备与人眼还是不可相媲美的。
不过,像素说明不了一切。实际上,人眼的高分辨率并不能覆盖在图像上的每一处细节。
这是由于进化的局限性。在长期的进化过程中,人类的注意力习惯性地会集中在中心位置——一般而言是盯紧猎物,而周围视野我们是用来防止狮子等捕食者靠近我们的,所以它不需要太清晰,能捕捉运动的物体就好了。
因此,我们的眼睛虽然看得很广,但其实它只能注意到中心部分的细节,而周围的细节其实只对运动物体有效。
在国外论坛上,有一位大神根据人眼看到的视角制作了一张人眼“拍出”的照片,它大概是这样子的:

我们的眼睛在距离中心20°之后,图像就变得不清晰,所以实际上,我们眼睛的像素要比理论推算的5.76亿低得多,大约只在500万到1500万像素之间。
当然,人眼与相机等技术设备相比仍然有一些不可替代的优势,比如我们对灰度的辨别能力是技术设备的两倍甚至更多,这一点是目前设备还无法超越我们的地方。
结语
眼睛是人类与外部世界沟通的桥梁,有了眼睛,我们才能发现外界的变动,并及时作出环境适应性行为;眼睛还是我们窥探美丽世界的一道窗口,透过这道窗,我们能看见生动鲜活的一草一木、繁华瑰丽的都市文化。
总之,眼睛对于我们至关重要,所以大家一定要爱惜眼睛、保护眼睛,不要让眼睛受到伤害。

0 人喜欢
暂无评论,来发布第一条评论吧!


