2.3亿年前,一场绵延200万年的大雨,把恐龙送上地球霸主的宝座
相信大家都知道,恐龙是地球上的一代霸主,它们在地球上称霸了长达1亿多年的时间,但或许你不知道的是,恐龙的崛起,与地球历史上的一次大规模、长时间的全球性降雨过程密切相关,简单来讲就是,在大约2.3亿年前,地球下了一场绵延200万年的大雨,把恐龙送上地球霸主的宝座。下面来我们看看这具体是怎么回事。
随着地球的板块运动,地球表面的海陆分布也在缓慢地变化,尽管对于我们人类来讲,这种变化可以说是微不可察,但如果把时间跨度拉长到上亿年的级别,那就不一样了。
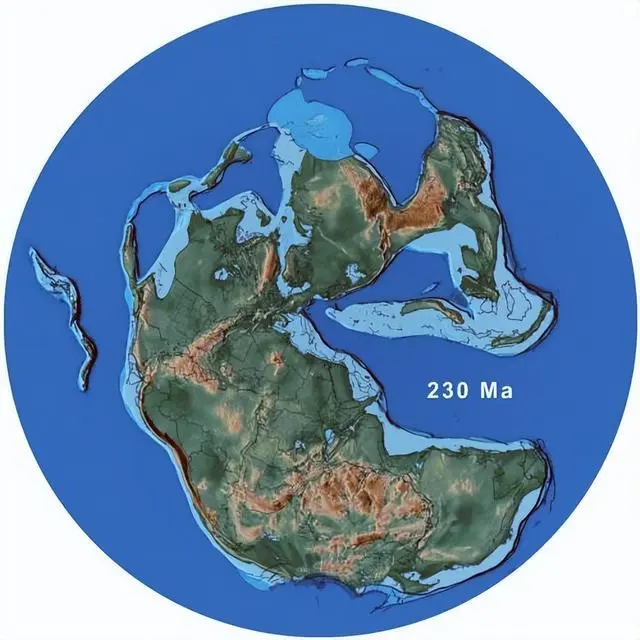
研究表明,在2.3亿年前的三叠纪,地球表面几乎所有的陆地都聚集在一起,形成了一片超级大陆,这也被称为“盘古大陆”(Pangea),在那个时候,由于来自海洋的湿润空气无法有效地深入到陆地深处,因此在“盘古大陆”内部的大片区域就很是干旱,并大量形成了一种红色砂石。
从上个世纪开始,科学家就陆陆续续地发现,在现代地球各大洲沿海区域的三叠纪地层中,广泛存在着包含这种红色砂石的沉积岩,科学家据此推测,这些现象应该是一次大规模、长时间的全球性降雨过程造成的,在此过程中,大量的降雨将原本只存在于陆地内部的红色砂石冲刷到了沿海区域。

与之对应的是,科学家还发现,在陆地内部区域同一时期的地层中,也普遍存在着一层薄薄的灰色岩层,其中含有大量的降雨痕迹,这无疑为这种观点提供了更多的证据。
在接下来的日子里,科学家又从地质记录、古生物化石记录、地球化学数据等方面进行了更深入地研究,最终确定了这次全球性降雨过程的存在,并通过放射性碳定年法,推算出这场大雨绵延了大约200万年的时间。
值得一提的是,这并不是说地球每个地方都一直都在下雨,而是说在这200万年的时间里,全球范围内的天气普遍以下雨为主,对于地球上大部分区域来讲,即使有时候会出现晴天,也很快会被下雨天代替。
此次全球性降雨过程被称为“卡尼期洪积事件”(Carnian Pluvial Episode),引人注目的是,这一时期的古生物化石表明,此次事件造成了当时地球上众多物种的一次规模较大的“洗牌”,一部分物种黯然退出了地球生命史的舞台,而另一部分物种则强势崛起,其中最具代表性的,就是后来的地球霸主——恐龙。

在2.3亿年前,恐龙已经在地球上出现,化石记录表明,在“卡尼期洪积事件”之前,恐龙的化石大概只占当时地球上陆地脊椎动物的5%左右,可以说是一种被边缘化的“角色”。
然而在“卡尼期洪积事件”期间,这一比例则一直在上升,以至于在“卡尼期洪积事件”结束之后,恐龙的化石在当时地球上陆地脊椎动物中所占的比例达到了大约90%之多。为什么会这样呢?科学家认为,最主要的原因就是当时地球陆地上的主要植物发生了巨大的变化。
在“卡尼期洪积事件”之前,地球陆地上的植物以耐旱的蕨类植物为主,例如节蕨、石松等,它们的植株低矮,其植物纤维易于被消化。
但在这场大雨的侵袭之下,蕨类植物遭到了重创,它们大片大片地消失,而取而代之的,则是那些耐水的裸子植物,例如松树、柏木、杉树等,与蕨类植物相比,它们的植株更高大,其植物纤维也粗糙得多。

对于习惯了以蕨类植物的植食动物来讲,这是一次非常严峻的考验,因为更加粗糙的植物纤维,就意味着难以消化,而相对容易消化的嫩叶,又会因为长在高处而吃不到,于是大量的植食动物都因为无法有效地消化裸子植物而灭绝,而接下来,习惯以这些植食动物为食的肉食动物也纷纷步入后尘……
但恐龙却经受起了这次考验,为什么呢?这是因为它们拥有更发达的牙齿和消化系统,可以有效地消化裸子植物的植物纤维,科学家发现,在那个时候,恐龙的胃里面就有具备研磨食物作用的胃石,除此之外,恐龙还可以直立起来,进而吃到一些长在高处的嫩叶,这无疑使它们的生存能力进一步增强。
一方面,大量的动物因为无法适应自然环境而日渐式微,另一方面,恐龙却可以在这样的自然环境中生存,此消彼长之下,恐龙就得以强势崛起,它们不断地向多样化发展,演化出包括食肉恐龙在内的各式各样的恐龙,并逐渐成为了地球上的一代霸主。

因此可以说,正是这一场绵延200万年的大雨,把恐龙送上地球霸主的宝座。那么问题就来了,为什么会有这一场大雨呢?
关于发生“卡尼期洪积事件”的原因,科学家提出过多种观点,其中认同度相对较高的观点认为,这应该是当时地球上的火山运动造成的。
科学家推测,在2.3亿年前,“盘古大陆”正在趋向于“裂开”,这导致了当时地球上的火山运动非常频繁,持续的火山运动将大量的二氧化碳源源不断地释放到大气层中,其产生的温室效应使得气温不断攀升。
在这种情况下,海洋的蒸发量也越来越大,进而造成强对流天气越来越频繁,范围也越来越大,与此同时,地球的大气层的气流也变得越来越强劲,在它们的驱动之下,大量的水汽不断地深入“盘古大陆”,当达到一定程度时,即使是“盘古大陆”最干旱的区域也下起了雨,于是一场大规模的全球性降雨过程就开始了。

尽管大量的降雨有助于降低地球的气温,同时还可以清除掉大气层中的一部分二氧化碳,这是因为二氧化碳会与水发生反应生成碳酸,而碳酸则会与其他的元素(如钙、镁等)进一步生成碳酸盐,但当时的火山运动却持续不停,它们会不断地向大气层中释放“新”的二氧化碳……
如此一来,就形成了一种动态的平衡,所以降雨过程就会一直持续,直到地球上的火山运动渐渐平息,这场绵延200万年的大雨才停了下来。
0 人喜欢
暂无评论,来发布第一条评论吧!